Công Thức Cấp Số Nhân Là Gì? Cách Tính Và Ứng Dụng Dễ Hiểu Nhất

Tìm hiểu công thức cấp số nhân là gì, cách tính số hạng và tổng, phân biệt với cấp số cộng và ứng dụng thực tế. Hãy cùng chúng tôi tìm hiểu thông qua bài viết dưới đây nhé!

Cấp số nhân là gì và khi nào bạn gặp nó trong cuộc sống

Hiểu đơn giản về cấp số nhân

Cấp số nhân là một dãy số mà mỗi số hạng (trừ số đầu tiên) đều được tạo thành bằng cách nhân số hạng trước với một số không đổi. Số không đổi này được gọi là công bội. Nếu bạn từng thấy một dãy số như 2, 4, 8, 16,… thì bạn đã bắt gặp cấp số nhân trong thực tế.

Mỗi số hạng sau lại gấp đôi số hạng trước, điều này thể hiện rõ đặc điểm “nhân lên” đều đặn của dãy. Không giống như cấp số cộng, nơi các số hạng tăng lên theo phép cộng, cấp số nhân lại phản ánh sự gia tăng theo bội số. Chính vì vậy, tốc độ tăng của nó thường nhanh hơn nhiều so với cấp số cộng.

Những tình huống thực tế có tính cấp số nhân

Cấp số nhân không chỉ xuất hiện trong sách giáo khoa mà còn hiện diện ở nhiều lĩnh vực. Một số ví dụ có thể kể đến như tốc độ phát triển dân số, sự lan truyền thông tin trên mạng xã hội, lãi suất kép trong tài chính, hoặc chuỗi phản ứng hóa học.

Khi bạn gửi tiết kiệm có lãi suất hàng năm và lãi đó tiếp tục được cộng dồn cho các năm sau, số tiền bạn có sẽ không tăng đều, mà tăng rất nhanh theo cấp số nhân. Đây là một khái niệm quan trọng trong các bài toán dự đoán và phân tích xu hướng.

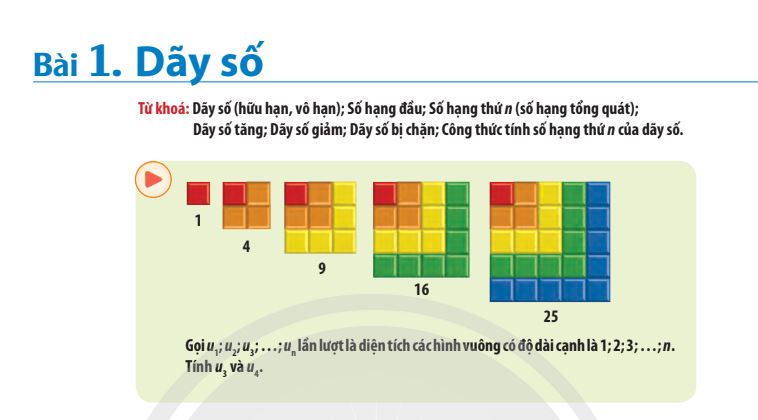
Dãy số tăng nhanh theo cấp số nhân

Công thức cấp số nhân và cách áp dụng chính xác

Cách tính số hạng bất kỳ trong cấp số nhân

Để xác định một số hạng cụ thể trong dãy cấp số nhân, bạn dùng công thức:

Un = a * q^(n – 1)

Trong đó, a là số hạng đầu tiên, q là công bội và n là vị trí của số hạng trong dãy. Giả sử bạn có dãy bắt đầu từ 5 và công bội là 3, số hạng thứ tư sẽ là 5 * 3^(4 – 1) = 135. Công thức cấp số nhân giúp bạn không cần phải viết ra cả dãy số, chỉ cần thay giá trị là ra kết quả.

Cách tính tổng nhiều số hạng đầu tiên

Để tính tổng của n số hạng đầu tiên trong cấp số nhân, bạn có thể áp dụng công thức:

Sn = a * (q^n – 1) / (q – 1) với q khác 1

Công thức này đặc biệt hữu ích trong các bài toán tính tổng đầu tư, tổng tiền sau nhiều kỳ lãi kép hoặc tổng khối lượng trong một chuỗi tăng trưởng.

Việc nhớ đúng công thức cấp số nhân và hiểu cách áp dụng sẽ giúp bạn giải nhanh các bài toán từ cơ bản đến nâng cao, đồng thời thấy được mối liên hệ của toán học với các tình huống trong đời thực.

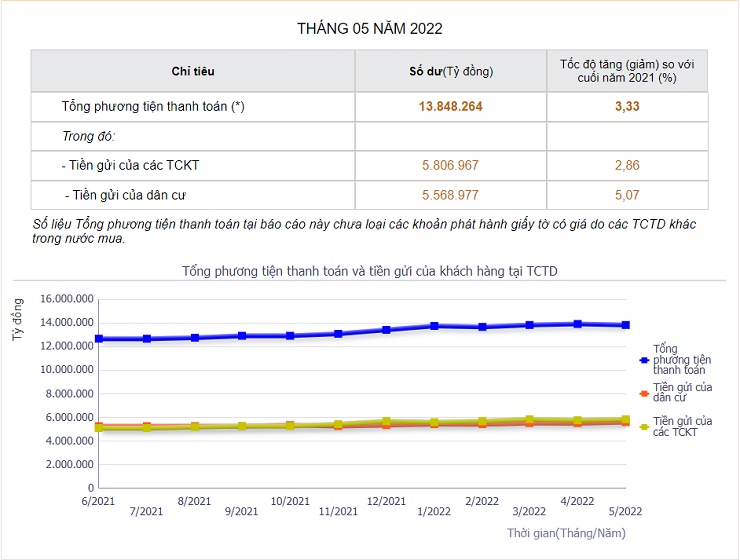
Sự tăng giá trị tài khoản tiết kiệm theo thời gian nhờ áp dụng cấp số nhân

So sánh cấp số nhân và cấp số cộng để không bị nhầm lẫn

Khác biệt trong cách tạo ra dãy số

Nhiều bạn thường nhầm lẫn giữa cấp số cộng và cấp số nhân do đều là các dãy số theo quy luật. Tuy nhiên, điểm khác biệt cốt lõi nằm ở phép tính. Cấp số cộng tạo ra dãy bằng cách cộng thêm một số cố định, còn cấp số nhân thì tạo ra số mới bằng phép nhân với một số không đổi.

Ví dụ, cấp số cộng có thể là 3, 6, 9, 12,… tăng dần theo công sai bằng 3. Trong khi đó, cấp số nhân như 2, 4, 8, 16,… lại nhân đôi liên tục. Tốc độ tăng trưởng của cấp số nhân nhanh hơn nhiều so với cấp số cộng, đặc biệt khi công bội lớn hơn 1.

Tác động đến kết quả và ứng dụng

Khi so sánh hai loại dãy số này, bạn sẽ thấy cấp số nhân thường được dùng trong các tình huống liên quan đến tăng trưởng mạnh, tăng trưởng theo chu kỳ hoặc hiện tượng nhân bản. Còn cấp số cộng lại thích hợp hơn với các tình huống mang tính tuyến tính, như tính khoảng cách hoặc tăng đều theo thời gian.

Nếu bạn hiểu rõ sự khác biệt này, bạn sẽ dễ dàng lựa chọn được công thức cấp số nhân hay cấp số cộng tùy vào yêu cầu của bài toán. Việc phân biệt đúng cũng giúp tránh những sai lầm thường gặp trong lúc giải toán.

Tác động của cấp số nhân trong việc lan truyền thông tin

Ứng dụng thực tế của cấp số nhân

Tài chính, đầu tư và tăng trưởng tài sản

Một trong những ứng dụng thực tế nổi bật nhất của công thức cấp số nhân chính là trong tài chính cá nhân và đầu tư. Khi bạn đầu tư vào một khoản sinh lời định kỳ và để lại lãi cộng dồn, khoản đầu tư của bạn sẽ không tăng tuyến tính mà sẽ tăng mạnh theo thời gian.

Ví dụ, bạn đầu tư 20 triệu đồng với lãi suất 10% mỗi năm, sau 5 năm, tổng số tiền sẽ là:

20 * (1.1)^5 = 32.21 triệu đồng

Sự tăng trưởng này không đơn thuần là cộng thêm 2 triệu mỗi năm, mà là lãi trên lãi – một đặc trưng của cấp số nhân.

Mạng xã hội, công nghệ và sinh học

Cấp số nhân cũng hiện diện rõ trong sự lan truyền của thông tin trên mạng xã hội. Một người chia sẻ, sau đó nhiều người khác chia sẻ lại, số lượng người tiếp cận nội dung đó tăng lên theo một dãy số nhân. Tương tự, tốc độ xử lý dữ liệu hoặc dung lượng ổ cứng cũng thường tăng gấp đôi sau mỗi vài năm, phản ánh định luật Moore trong ngành công nghệ.

Ngoài ra, trong sinh học, sự nhân đôi tế bào hoặc sự phát triển của quần thể vi khuẩn cũng tuân theo quy luật cấp số nhân. Đó là lý do vì sao việc kiểm soát sự lây lan của virus là điều cực kỳ quan trọng, bởi nếu để tự do, số lượng ca bệnh có thể tăng nhanh không thể kiểm soát.

Việc hiểu rõ và áp dụng công thức cấp số nhân sẽ giúp bạn có cái nhìn logic và sâu sắc hơn về nhiều hiện tượng trong toán học và cuộc sống. Từ những dãy số đơn giản trong sách giáo khoa, đến những mô hình tăng trưởng thực tế như tài chính, công nghệ, sinh học – tất cả đều gắn chặt với khái niệm này. Hãy tiếp tục luyện tập và vận dụng nó một cách linh hoạt, để biến kiến thức thành công cụ phục vụ cuộc sống mỗi ngày.