Học nhanh công thức cấp số nhân và bài tập có lời giải

Định nghĩa cấp số nhân

Cấp số nhân là một dãy số trong đó mỗi số hạng (kể từ số hạng thứ hai) đều bằng số hạng liền trước nhân với một hằng số không đổi, gọi là công bội.

 

Nói một cách dễ hiểu, đây là dãy số mà tỷ lệ giữa hai số hạng liên tiếp luôn bằng nhau. Ví dụ, dãy 2, 4, 8, 16, 32,… là một cấp số nhân vì mỗi số hạng sau luôn gấp đôi số hạng trước, tức công bội ở đây là 2.

Đặc điểm quan trọng của cấp số nhân:

 

Các số hạng thay đổi theo tỷ lệ nhân chứ không phải tỷ lệ cộng như cấp số cộng.

 

Công bội có thể là số dương, số âm hoặc số thập phân; khi đó dãy có thể tăng, giảm hoặc xen kẽ dấu.

 

Nhờ tính chất nhân liên tiếp, cấp số nhân thường được áp dụng để mô tả sự tăng trưởng hoặc giảm sút theo tỷ lệ cố định, như lãi suất kép, sự suy giảm phóng xạ hoặc các bài toán lũy thừa.

Học sinh trong giờ toán

Công thức cơ bản trong cấp số nhân

Cấp số nhân là một dãy số mà mỗi số hạng, bắt đầu từ số thứ hai, đều bằng số hạng liền trước nhân với một hằng số không đổi gọi là công bội. Nhờ cấu trúc đặc biệt này, cấp số nhân có một số công thức cấp số nhân cơ bản rất quan trọng, giúp tính toán nhanh và hiệu quả.

 

Công thức tính số hạng tổng quát

Để tìm số hạng thứ n trong một cấp số nhân, ta dùng công thức cấp số nhân:

un = u1 × q^(n-1)

 

Trong đó:

 

u1: số hạng đầu tiên

 

q: công bội

 

n: vị trí số hạng cần tính

 

Công thức tính tổng n số hạng đầu tiên

Tổng của n số hạng đầu tiên của cấp số nhân:

 

Khi q ≠ 1:

Sn = u1 × (q^n – 1) / (q – 1)

 

Khi q = 1:

Sn = u1 × n

 

Trong đó:

 

Sn: tổng của n số hạng đầu tiên

 

q: công bội

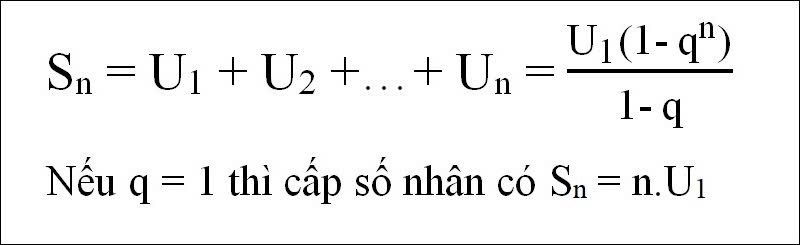
Công thức cơ bản

Công thức tính công bội

Khi biết hai số hạng bất kỳ um và un:

q = căn bậc (n – m) của (un / um)

 

Những công thức cấp số nhân trên thường được dùng để tính nhanh số hạng hoặc tổng của cấp số nhân, đồng thời ứng dụng trong nhiều bài toán thực tế như tính lãi suất kép, tăng trưởng dân số hay phân rã chất phóng xạ.

 

Các dạng bài tập thường gặp về cấp số nhân

Trong chương trình Toán học, đặc biệt ở bậc trung học phổ thông, cấp số nhân thường xuất hiện dưới nhiều dạng bài tập đa dạng. Việc nắm rõ từng dạng giúp bạn dễ dàng nhận diện và giải nhanh hơn.

 

Tính số hạng bất kỳ trong cấp số nhân

Dạng bài này thường cho biết số hạng đầu tiên và công bội, hoặc cho hai số hạng bất kỳ rồi yêu cầu tính số hạng thứ n. Áp dụng công thức cơ bản un = u1 × q^(n-1).

 

Tính công bội của cấp số nhân

Bài toán có thể cung cấp hai số hạng khác nhau như um và un, yêu cầu tính công bội q. Công thức thường dùng là: q = căn bậc (n – m) của (un / um).

 

Tính tổng n số hạng đầu tiên

Đây là dạng phổ biến, yêu cầu tính Sn dựa trên u1 và q. Công thức áp dụng là: Sn = u1 × (q^n – 1) / (q – 1) nếu q ≠ 1.

 

Tìm số hạng đầu tiên hoặc số hạng chưa biết

Cho biết tổng, công bội và một số điều kiện khác, yêu cầu tìm u1 hoặc số hạng nào đó. Dạng này cần linh hoạt kết hợp các công thức cấp số nhân và giải phương trình.

 

Nhận biết cấp số nhân và chứng minh dãy là cấp số nhân

Đề thường cho dãy số, yêu cầu chứng minh tỉ lệ giữa hai số hạng liên tiếp bằng nhau, từ đó kết luận đó là cấp số nhân.

 

Giải bài toán ứng dụng thực tế

Dạng này thường mô phỏng các tình huống như gửi tiết kiệm lãi kép, sự tăng trưởng dân số, giảm giá trị theo năm… Mục đích giúp học sinh thấy được tính ứng dụng của cấp số nhân.

Ứng dụng cấp số nhân trong thực tế

Cấp số nhân không chỉ xuất hiện trong sách giáo khoa Toán học mà còn gắn liền với nhiều hiện tượng, quy luật tự nhiên và lĩnh vực kinh tế, kỹ thuật trong cuộc sống hàng ngày. Việc nhận ra và hiểu được ứng dụng của cấp số nhân giúp chúng ta giải quyết các bài toán thực tế nhanh và hiệu quả hơn.

 

Tính lãi suất kép trong ngân hàng

Một trong những ứng dụng phổ biến nhất của cấp số nhân là tính lãi suất kép. Khi gửi tiền tiết kiệm với lãi suất cố định, số tiền lãi sẽ tiếp tục được cộng dồn vào gốc và sinh lãi ở các kỳ tiếp theo. Kết quả là số tiền tăng theo cấp số nhân, chứ không tăng đều như cộng thêm một số cố định.

 

Mô hình tăng trưởng dân số

Trong nhiều trường hợp, tốc độ tăng trưởng dân số được giả định tỷ lệ thuận với quy mô dân số hiện tại, tạo ra một chuỗi số liệu có dạng cấp số nhân. Đây cũng là nguyên lý giúp các nhà nghiên cứu dự đoán dân số trong tương lai.

 

Hiện tượng phóng xạ hoặc hao mòn tự nhiên

Khi một chất phóng xạ phân rã hoặc vật thể bị ăn mòn theo tỷ lệ phần trăm cố định qua mỗi khoảng thời gian, khối lượng còn lại giảm dần theo cấp số nhân. Công thức cấp số nhân giúp tính toán nhanh giá trị còn lại sau một thời gian dài.

 

Chi phí sản xuất và quy mô kinh tế

Trong một số ngành sản xuất, khi quy mô mở rộng, chi phí hoặc doanh thu có thể tăng theo cấp số nhân. Việc dự báo lợi nhuận, chi phí dựa trên mô hình cấp số nhân giúp doanh nghiệp lập kế hoạch đầu tư và mở rộng hợp lý.

 

Mạng lưới, truyền thông và công nghệ

Trong thế giới công nghệ, số lượng người dùng, lượt chia sẻ, lan truyền thông tin trên mạng xã hội có thể tăng nhanh theo cấp số nhân, nhất là khi nội dung trở thành “viral”.

Ứng dụng nhiều vào đời sống

Mẹo ghi nhớ và tránh sai lầm khi dùng công thức cấp số nhân

Cấp số nhân không quá khó nhưng nhiều học sinh dễ nhầm lẫn giữa công thức tính số hạng, công bội và tổng. Dưới đây là một số mẹo đơn giản giúp ghi nhớ lâu hơn và hạn chế những sai sót thường gặp.

 

Hiểu ý nghĩa thay vì chỉ học thuộc

Thay vì chỉ nhớ máy móc công thức un = u1 × q^(n-1), hãy hình dung số hạng thứ n chính là số hạng đầu tiên nhân liên tiếp với công bội (n – 1) lần. Việc hiểu bản chất sẽ giúp bạn tự suy ra công thức khi quên.

 

Nhớ công thức tổng dựa trên cấu trúc

Với tổng n số hạng đầu tiên, công thức Sn = u1 × (q^n – 1) / (q – 1) thực chất xuất phát từ việc cộng dồn từng số hạng. Hãy để ý dấu hiệu đặc trưng là “(q^n – 1)” nằm trên tử, và “q – 1” nằm dưới mẫu.

 

Kiểm tra kỹ công bội trước khi áp dụng

Một sai lầm phổ biến là áp dụng sai giá trị công bội q, đặc biệt khi q là số âm hoặc phân số. Hãy luôn tính và kiểm tra q bằng cách lấy một số hạng chia cho số hạng liền trước để tránh nhầm dấu hoặc trị số.

 

Xác định rõ vị trí số hạng đầu tiên

Nhiều bạn thường nhầm lẫn giữa u1 và số hạng ở một vị trí khác. Nên nhớ, công thức un = u1 × q^(n-1) chỉ đúng khi u1 thực sự là số hạng đầu tiên của dãy.

 

Viết lại công thức ra nháp trước khi tính toán

Khi làm bài tập, đừng vội tính nhẩm mà nên viết rõ công thức ra giấy. Việc này giúp hạn chế quên số mũ (n-1) hoặc quên dấu ngoặc, vốn là lỗi rất hay gặp.

 

Kiểm tra kết quả xem có hợp lý không

Cuối cùng, sau khi tính toán, hãy so sánh kết quả với tính chất của dãy: nếu công bội lớn hơn 1 thì dãy phải tăng dần; nếu công bội là số âm thì số hạng phải xen kẽ âm – dương; nếu công bội nhỏ hơn 1 (nhưng dương) thì dãy giảm dần. Đây là bước giúp phát hiện lỗi tính nhanh nhất.