Mục lục

Công thức cấp số nhân là một phần kiến thức quan trọng trong chương trình toán học, giúp giải nhanh các bài toán liên quan đến dãy số. Hiểu rõ và vận dụng thành thạo công thức cấp số nhân sẽ giúp bạn tính số hạng, tổng dãy chính xác, tiết kiệm thời gian.

Công thức cấp số nhân

Cấp số nhân là gì?

Cấp số nhân là một dãy số mà kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng liền trước nhân với một hằng số khác 0, gọi là công bội.

Cụ thể, dãy số u₁, u₂, u₃, …, uₙ là một cấp số nhân nếu tồn tại một số q ≠ 0 sao cho:
uₙ = uₙ₋₁ × q với mọi n > 1

Trong đó:

u₁ là số hạng đầu tiên.
q là công bội, được tính bằng tỉ số giữa hai số hạng liên tiếp: q = u₂ / u₁.

Ví dụ:
Dãy số 3, 6, 12, 24, 48 là một cấp số nhân với công bội q = 2, vì mỗi số hạng gấp đôi số hạng trước.

Công thức cấp số nhân — Cấp số nhân là gì?

Dấu hiệu nhận biết một dãy số là cấp số nhân?

Một dãy số được gọi là cấp số nhân khi kể từ số hạng thứ hai, tỉ số giữa một số hạng và số hạng liền trước luôn bằng nhau và bằng một hằng số khác 0, gọi là công bội.

Cụ thể:
Dãy số u₁, u₂, u₃, …, uₙ là cấp số nhân nếu:
u₂ / u₁ = u₃ / u₂ = … = uₙ / uₙ₋₁ = q (q ≠ 0)

Trong đó:

q là công bội, đặc trưng của cấp số nhân.
Tỉ số q phải không đổi trong suốt dãy số.

Ví dụ:
Dãy 2, 4, 8, 16, 32 là cấp số nhân vì: 4/2 = 8/4 = 16/8 = 32/16 = 2 (công bội q = 2)

Như vậy, để kiểm tra một dãy số có phải là cấp số nhân hay không, chỉ cần tính tỉ số giữa hai số hạng liên tiếp bất kỳ và kiểm tra xem các tỉ số này có bằng nhau hay không.

Công thức cấp số nhân và cách áp dụng giải nhanh các bài toán

Cấp số nhân là dạng dãy số đặc biệt, trong đó mỗi số hạng (kể từ số thứ hai) bằng số hạng liền trước nhân với một hằng số không đổi, gọi là công bội. Nắm vững công thức của cấp số nhân giúp bạn giải nhanh các dạng bài toán liên quan đến dãy số, tìm số hạng, tổng dãy hoặc kiểm tra tính chất của dãy.

Số hạng tổng quát của công thức cấp số nhân:

uₙ = u₁ × qⁿ⁻¹
Trong đó:

u₁: số hạng đầu tiên
q: công bội, tính theo q = u₂ / u₁
n: số thứ tự của số hạng cần tìm

Công bội q:

q = u₂ / u₁ hoặc q = uₙ / uₙ₋₁ (với n > 1)
Lưu ý: công bội q ≠ 0.

Tổng n số hạng đầu tiên (với q ≠ 1):

Sₙ = u₁ × (qⁿ – 1) / (q – 1)

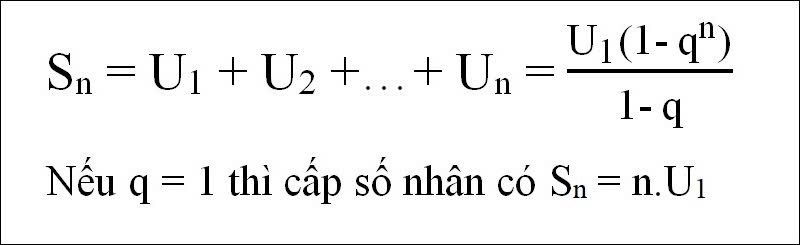
Tổng cấp số nhân vô hạn hội tụ:

Nếu |q| < 1 (tức là q nằm trong khoảng từ -1 đến 1, không kể 0), tổng của dãy vô hạn là:
S = u₁ / (1 – q)

Cách áp dụng công thức để giải nhanh các bài toán:

Xác định số hạng đầu tiên u₁ và công bội q.
Kiểm tra xem dãy hữu hạn hay vô hạn, hội tụ hay không.
Áp dụng đúng công thức tương ứng với yêu cầu đề bài.
Chú ý điều kiện của q để tránh sai sót.

Ví dụ minh họa:

Bài 1: Cho dãy số 2, 6, 18, 54. Tính số hạng thứ 6.
Giải:
u₁ = 2, q = 6 / 2 = 3
u₆ = u₁ × q⁵ = 2 × 3⁵ = 486

Bài 2: Cho dãy số 5, 10, 20, 40, … Tính tổng 6 số hạng đầu tiên.
Giải:
u₁ = 5, q = 2, n = 6
S₆ = 5 × (2⁶ – 1) / (2 – 1) = 5 × (64 – 1) = 315

Bài 3: Một cấp số nhân có u₁ = 100, công bội q = 0,5. Tính tổng vô hạn của dãy.
Giải:
Vì |q| = 0,5 < 1 nên dãy hội tụ.
S = 100 / (1 – 0,5) = 200

Bài 4: Cho dãy 81, 27, 9, 3, … Tìm số hạng thứ 5.
Giải:
u₁ = 81, q = 27 / 81 = 1/3
u₅ = 81 × (1/3)⁴ = 1

Các công thức của cấp số nhân rất quan trọng và thường xuyên xuất hiện trong các bài toán số học, đại số, tài chính. Việc nắm chắc các công thức trên và cách áp dụng hợp lý sẽ giúp bạn giải nhanh và chính xác.

Những sai lầm thường gặp khi tính toán cấp số nhân?

Khi giải các bài toán liên quan đến cấp số nhân, nhiều học sinh và người học dễ mắc phải một số sai lầm cơ bản khiến kết quả tính toán sai lệch. Dưới đây là những sai lầm thường gặp nhất cần lưu ý để tránh:

Xác định sai công bội q
Rất nhiều người nhầm lẫn cách tính công bội q, nhất là khi dãy số có số hạng âm hoặc phân số. Công bội q luôn được tính bằng tỉ số của số hạng sau chia cho số hạng trước:
q = u₂ / u₁
Nếu tính q sai ngay từ đầu, toàn bộ các số hạng và tổng dãy tính ra đều sai.

Ví dụ:
Dãy 8, 4, 2, 1…
Nhiều bạn tính q = 4 – 8 = -4 (sai), trong khi đúng là q = 4 / 8 = 0,5.

Nhầm lẫn với cấp số cộng
Một số học sinh nhầm lẫn cấp số nhân với cấp số cộng, dẫn đến cộng công sai thay vì nhân công bội. Ví dụ: cho dãy 2, 4, 8, 16…, nhiều bạn tính u₄ = u₁ + 3q thay vì u₄ = u₁ × q³.

Dùng sai công thức tính tổng Sₙ
Công thức tính tổng n số hạng đầu tiên chỉ đúng khi q ≠ 1. Nếu q = 1, tổng dãy chỉ là: Sₙ = n × u₁.
Ngoài ra, khi dãy vô hạn, chỉ được dùng công thức tổng vô hạn nếu |q| < 1, nếu không dãy sẽ không hội tụ.

Sai dấu mũ hoặc chỉ số
Khi tính số hạng tổng quát uₙ = u₁ × qⁿ⁻¹, nhiều bạn quên trừ 1 ở số mũ hoặc nhầm thành qⁿ, dẫn đến kết quả sai. Cần chú ý công thức chuẩn.

Thiếu điều kiện kiểm tra hội tụ trong dãy vô hạn
Khi tính tổng cấp số nhân vô hạn, nhiều bạn không kiểm tra điều kiện |q| < 1 mà vẫn tính tổng, dẫn đến kết quả sai vì dãy không hội tụ.

Lời khuyên:
Để tránh những sai lầm trên, khi làm bài cần:

Xác định chính xác u₁ và q.
Phân biệt rõ cấp số nhân với cấp số cộng.
Kiểm tra điều kiện của q trước khi áp dụng công thức tổng.
Viết đúng công thức, cẩn thận với chỉ số mũ.

Việc luyện tập nhiều dạng bài tập với các trường hợp đặc biệt cũng giúp bạn tự tin hơn khi xử lý các bài toán cấp số nhân.

Rate this post