Diện tích xung quanh hình nón: Công thức và cách tính dễ hiểu

Diện tích xung quanh hình nón là kiến thức hình học quan trọng trong chương trình Toán học, giúp học sinh hiểu rõ về bề mặt bên của hình nón và cách tính diện tích chính xác. Nội dung này thường xuất hiện trong bài tập và các ứng dụng thực tế. Để nắm vững kiến thức, cùng tìm hiểu qua bài viết dưới đây.

Diện tích xung quanh hình nón​

Diện tích xung quanh của hình nón là gì?

Diện tích xung quanh của hình nón là phần diện tích của mặt cong bao quanh hình nón, không bao gồm diện tích đáy. Đây là diện tích của bề mặt bên khi trải hình nón ra mặt phẳng, thường có dạng một hình quạt tròn.

Trong hình học, diện tích xung quanh của hình nón được dùng để:

• Tính diện tích phần bề mặt bên của các vật có dạng hình nón 
• Phục vụ cho việc giải các bài toán hình học không gian 
• Ứng dụng trong thực tế như tính diện tích làm mũ nón, phễu, ốc quế, mái nhà hình nón… 

Các yếu tố liên quan đến diện tích xung quanh của hình nón

Để hiểu rõ diện tích xung quanh của hình nón, cần nắm các đại lượng sau:

• Bán kính đáy (r): khoảng cách từ tâm đáy đến mép đáy 
• Đường sinh (l): độ dài cạnh bên của hình nón, nối từ đỉnh đến một điểm trên đường tròn đáy 

Diện tích xung quanh của hình nón phụ thuộc trực tiếp vào bán kính đáy và đường sinh, không phụ thuộc vào chiều cao của hình nón.

Diện tích xung quanh của hình nón là phần diện tích mặt cong bao quanh hình nón, đóng vai trò quan trọng trong học tập và ứng dụng thực tế. Việc hiểu đúng khái niệm này sẽ giúp bạn dễ dàng áp dụng công thức và giải chính xác các bài toán liên quan.

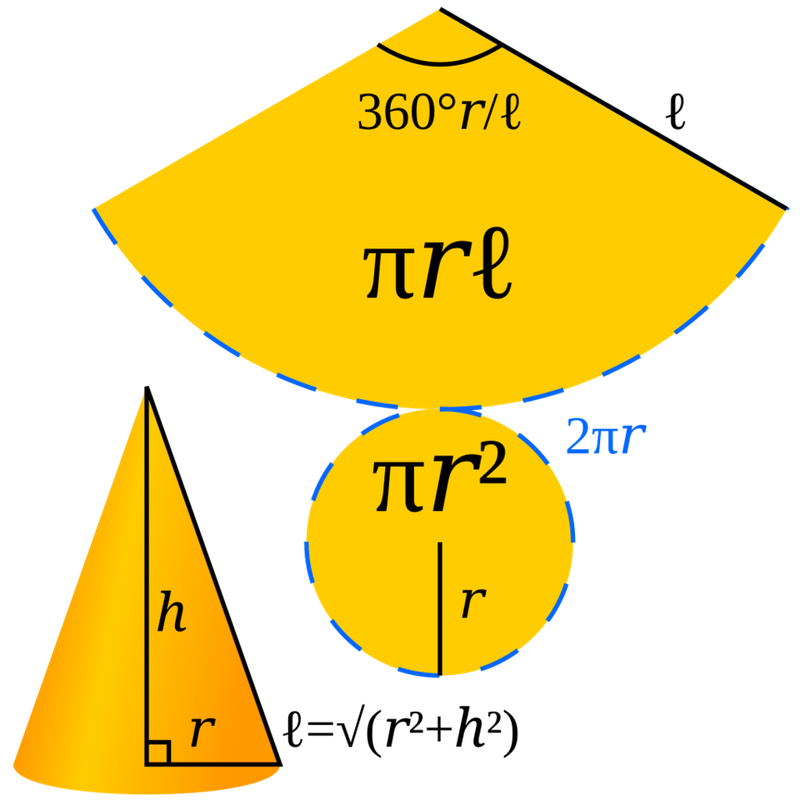
Công thức tính diện tích xung quanh của hình nón chuẩn nhất

Diện tích xung quanh của hình nón được tính dựa trên bán kính đáy và đường sinh của hình nón. Đây là công thức chuẩn, được sử dụng thống nhất trong chương trình Toán học.

Công thức tính

Diện tích xung quanh của hình nón được xác định theo công thức:

Sxq = π × r × l

Trong đó:

• Sxq: Diện tích xung quanh của hình nón 
• π (pi): Hằng số, xấp xỉ 3,14 
• r: Bán kính đáy hình nón 
• l: Đường sinh của hình nón 

Lưu ý khi áp dụng công thức

• Bán kính đáy và đường sinh phải cùng đơn vị đo 
• Kết quả diện tích được tính theo đơn vị diện tích (cm², m², …) 
• Không nhầm lẫn đường sinh l với chiều cao h của hình nón 

Khi nào sử dụng công thức này?

Công thức diện tích xung quanh của hình nón được dùng khi:

• Cần tính diện tích mặt bên của hình nón 
• Bài toán không yêu cầu tính diện tích đáy 
• Giải các bài toán thực tế liên quan đến vật thể có dạng hình nón
  

 

Công thức Sxq = π × r × l là công thức chuẩn và quan trọng để tính diện tích xung quanh của hình nón. Việc hiểu rõ ý nghĩa các đại lượng trong công thức sẽ giúp bạn áp dụng chính xác và tránh sai sót khi làm bài.

Cách tính diện tích xung quanh hình nón chi tiết từng bước

Để tính diện tích xung quanh của hình nón chính xác, bạn chỉ cần thực hiện theo đúng trình tự các bước dưới đây. Cách làm này phù hợp cho học sinh và dễ áp dụng trong mọi dạng bài tập.

Bước 1: Xác định các yếu tố của hình nón

Trước tiên, cần xác định rõ các đại lượng đã cho trong bài toán:

• Bán kính đáy (r) của hình nón 
• Đường sinh (l) của hình nón 

⚠️ Lưu ý: Nếu bài toán chỉ cho chiều cao (h) và bán kính đáy, bạn cần tính đường sinh trước theo định lý Pythagore:
l = √(r² + h²)

Bước 2: Ghi đúng công thức tính

Công thức tính diện tích xung quanh của hình nón là:
Sxq = π × r × l

Trong đó π ≈ 3,14.

Bước 3: Thay số vào công thức

Thay các giá trị của bán kính đáy và đường sinh đã xác định vào công thức.
Đảm bảo các đại lượng cùng đơn vị đo để tránh sai sót.

Bước 4: Thực hiện phép tính

Tiến hành nhân các số theo đúng thứ tự:

• Nhân r với l 
• Nhân kết quả với π 

Sau đó ghi kết quả kèm đơn vị diện tích (cm², m²,…).

Bước 5: Kết luận và kiểm tra lại

• Kiểm tra phép tính 
• Kiểm tra đơn vị đo 
• Đảm bảo không nhầm lẫn diện tích xung quanh với diện tích toàn phần 

Ví dụ minh họa

Cho hình nón có bán kính đáy r = 3 cm, đường sinh l = 5 cm.
Diện tích xung quanh là:
Sxq = 3,14 × 3 × 5 = 47,1 cm²

Chỉ cần thực hiện đúng 5 bước trên, bạn có thể tính diện tích xung quanh của hình nón nhanh chóng và chính xác. Việc nắm vững quy trình sẽ giúp bạn tránh nhầm lẫn và làm tốt các dạng bài toán liên quan.

Bài tập ví dụ và lỗi thường gặp khi tính diện tích xung quanh hình nón

Để nắm vững cách tính diện tích xung quanh của hình nón, bạn nên luyện tập qua các ví dụ cụ thể và nhận biết những lỗi sai phổ biến. Điều này giúp tránh nhầm lẫn và nâng cao độ chính xác khi làm bài.

Bài tập ví dụ 1

Bài toán:
Cho hình nón có bán kính đáy r = 4 cm, đường sinh l = 7 cm. Tính diện tích xung quanh của hình nón.

Lời giải:
Áp dụng công thức:
Sxq = π × r × l
= 3,14 × 4 × 7
= 87,92 cm²

Kết luận:
Diện tích xung quanh của hình nón là 87,92 cm².

Bài tập ví dụ 2

Bài toán:
Cho hình nón có bán kính đáy r = 6 cm, chiều cao h = 8 cm. Tính diện tích xung quanh của hình nón.

Lời giải:
Trước tiên tính đường sinh:
l = √(r² + h²) = √(6² + 8²) = √100 = 10 cm

Diện tích xung quanh:
Sxq = π × r × l
= 3,14 × 6 × 10
= 188,4 cm²

Kết luận:
Diện tích xung quanh của hình nón là 188,4 cm².

Những lỗi thường gặp khi tính diện tích xung quanh hình nón

Nhầm lẫn giữa đường sinh và chiều cao
Nhiều học sinh dùng chiều cao h thay cho đường sinh l, dẫn đến kết quả sai.

Quên tính đường sinh khi bài cho chiều cao
Khi chỉ có r và h, cần tính l trước rồi mới áp dụng công thức.

Nhầm công thức diện tích xung quanh và diện tích toàn phần
Diện tích xung quanh: π × r × l
Diện tích toàn phần: π × r × l + π × r²

Sai đơn vị đo
Không đổi các đại lượng về cùng một đơn vị trước khi tính.

Quên ghi đơn vị diện tích
Kết quả cuối cùng phải kèm đơn vị như cm², m²,…

Kết luận

Thông qua các bài tập ví dụ và việc nhận diện lỗi thường gặp, bạn sẽ hiểu rõ hơn cách tính diện tích xung quanh của hình nón và tránh được những sai sót không đáng có. Luyện tập thường xuyên sẽ giúp bạn làm bài nhanh và chính xác hơn.