Diện tích toàn phần hình trụ: Công thức và cách tính chi tiết

Diện tích toàn phần hình trụ là kiến thức hình học quan trọng trong chương trình Toán học, giúp học sinh hiểu rõ diện tích bề mặt của hình trụ và cách tính chính xác. Nội dung này thường xuất hiện trong các bài tập và ứng dụng thực tế. Để nắm vững kiến thức, cùng tìm hiểu qua bài viết dưới đây.

 

Diện tích toàn phần hình trụ​

Diện tích toàn phần hình trụ là gì?

Diện tích toàn phần của hình trụ là tổng diện tích của toàn bộ bề mặt hình trụ, bao gồm diện tích xung quanh và diện tích hai mặt đáy. Đây là khái niệm quan trọng trong hình học không gian, thường xuất hiện trong các bài toán Toán học và các ứng dụng thực tế.

Cụ thể, diện tích toàn phần của hình trụ gồm:

• Diện tích xung quanh: là diện tích mặt cong bao quanh hình trụ

• Diện tích hai mặt đáy: là diện tích của hai hình tròn đáy bằng nhau

Các yếu tố liên quan đến diện tích toàn phần của hình trụ

Để tính diện tích toàn phần của hình trụ, cần xác định:

• Bán kính đáy (r): khoảng cách từ tâm đến mép đáy

• Chiều cao (h): khoảng cách giữa hai mặt đáy

Diện tích toàn phần của hình trụ phụ thuộc trực tiếp vào bán kính đáy và chiều cao, không phụ thuộc vào vị trí đặt hình trụ.

Ứng dụng của diện tích toàn phần của hình trụ

Diện tích toàn phần của hình trụ được sử dụng để:

• Tính diện tích vật liệu cần dùng khi bọc, sơn hoặc phủ kín vật thể dạng hình trụ

• Giải các bài toán liên quan đến lon nước, ống trụ, bể chứa hình trụ…

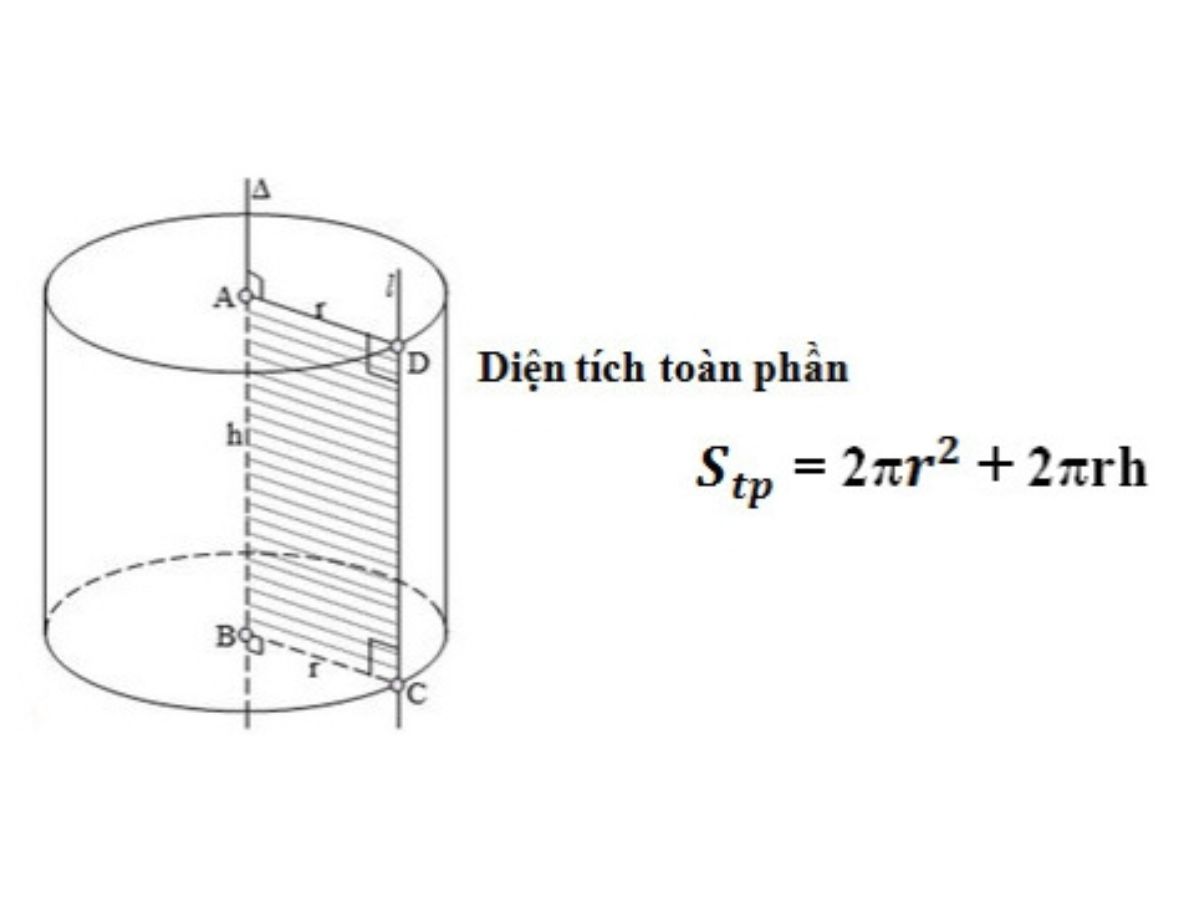
Công thức tính diện tích toàn phần hình trụ chuẩn nhất

Diện tích toàn phần của hình trụ được tính bằng tổng diện tích xung quanh và diện tích hai mặt đáy. Đây là công thức chuẩn, được sử dụng thống nhất trong chương trình Toán học.

Công thức tính

Công thức tính diện tích toàn phần của hình trụ là:

Stp = 2πr h + 2πr²

Trong đó:

• Stp: Diện tích toàn phần của hình trụ

• π (pi): Hằng số, xấp xỉ 3,14

• r: Bán kính đáy hình trụ

• h: Chiều cao hình trụ

Giải thích công thức

• 2πr h là diện tích xung quanh hình trụ

• 2πr² là diện tích của hai mặt đáy

Cộng hai phần này lại ta được diện tích toàn phần của hình trụ.

Lưu ý khi áp dụng công thức

• Bán kính và chiều cao phải cùng đơn vị đo

• Kết quả phải ghi đơn vị diện tích (cm², m², …)

• Không nhầm lẫn với công thức diện tích xung quanh hình trụ

Cách tính diện tích toàn phần của hình trụ chi tiết từng bước

Để tính diện tích toàn phần của hình trụ chính xác, bạn chỉ cần thực hiện theo đúng các bước dưới đây. Cách làm này giúp tránh nhầm lẫn và phù hợp cho mọi dạng bài tập.

Bước 1: Xác định các yếu tố của hình trụ

Trước tiên, cần xác định rõ các đại lượng đã cho trong bài toán:

• Bán kính đáy (r)

• Chiều cao (h)

Đảm bảo r và h cùng đơn vị đo trước khi tính.

Bước 2: Ghi đúng công thức tính

Công thức tính diện tích toàn phần của hình trụ là:
Stp = 2πr h + 2πr²

Trong đó:

• 2πr h: diện tích xung quanh

• 2πr²: diện tích hai mặt đáy

Bước 3: Thay số vào công thức

Thay giá trị bán kính đáy và chiều cao vào công thức đã ghi.
Lưu ý thay đúng vị trí để tránh nhầm lẫn giữa các đại lượng.

Bước 4: Thực hiện phép tính

Tiến hành tính lần lượt:

• Tính diện tích xung quanh

• Tính diện tích hai mặt đáy

• Cộng hai kết quả lại với nhau

Sử dụng π ≈ 3,14 nếu đề bài không yêu cầu giá trị khác.

Bước 5: Kiểm tra và kết luận

• Kiểm tra lại phép tính

• Ghi đầy đủ đơn vị diện tích (cm², m², …)

• Đảm bảo không nhầm với diện tích xung quanh hình trụ

Ví dụ minh họa

Cho hình trụ có bán kính đáy r = 5 cm, chiều cao h = 10 cm.
Diện tích toàn phần là:

Stp = 2 × 3,14 × 5 × 10 + 2 × 3,14 × 5²
= 314 + 157
= 471 cm²

 

Thực hiện đúng 5 bước trên sẽ giúp bạn tính diện tích toàn phần của hình trụ nhanh và chính xác. Việc nắm vững quy trình này rất cần thiết để làm tốt các bài toán hình học liên quan.

Phân biệt diện tích toàn phần và diện tích xung quanh hình trụ

Trong hình học không gian, diện tích toàn phần của hình trụ và diện tích xung quanh hình trụ là hai khái niệm dễ gây nhầm lẫn. Việc phân biệt rõ sẽ giúp bạn áp dụng đúng công thức và làm bài chính xác hơn.

Diện tích xung quanh hình trụ là gì?

Diện tích xung quanh hình trụ là diện tích của mặt cong bao quanh hình trụ, không bao gồm hai mặt đáy.

• Công thức:
  Sxq = 2πr h

• Phụ thuộc vào:
  • Bán kính đáy (r)

  • Chiều cao (h)

• Ứng dụng:
  • Tính diện tích bọc, sơn phần mặt bên của hình trụ

Diện tích toàn phần của hình trụ là gì?

Diện tích toàn phần của hình trụ là tổng diện tích xung quanh và diện tích hai mặt đáy của hình trụ.

• Công thức:
  Stp = 2πr h + 2πr²

• Bao gồm:
  • Diện tích mặt xung quanh

  • Diện tích của hai hình tròn đáy

• Ứng dụng:
  • Tính diện tích vật liệu cần phủ kín toàn bộ hình trụ

So sánh diện tích toàn phần và diện tích xung quanh hình trụ

• Diện tích xung quanh chỉ tính mặt bên, không có đáy

• Diện tích toàn phần tính cả mặt bên và hai mặt đáy

• Công thức diện tích toàn phần luôn lớn hơn diện tích xung quanh

Hiểu rõ sự khác nhau giữa diện tích toàn phần và diện tích xung quanh hình trụ sẽ giúp bạn tránh nhầm lẫn khi làm bài tập và áp dụng công thức đúng trong từng trường hợp cụ thể.

Bài tập ví dụ và lỗi thường gặp khi tính diện tích toàn phần hình trụ

Để hiểu rõ và vận dụng đúng cách tính diện tích toàn phần của hình trụ, bạn cần luyện tập qua các ví dụ cụ thể và tránh những lỗi sai phổ biến dưới đây.

Bài tập ví dụ 1

Bài toán:
Cho hình trụ có bán kính đáy r = 3 cm, chiều cao h = 7 cm. Tính diện tích toàn phần của hình trụ.

Lời giải:
Áp dụng công thức:
Stp = 2πr h + 2πr²

Thay số:
Stp = 2 × 3,14 × 3 × 7 + 2 × 3,14 × 3²
= 131,88 + 56,52
= 188,4 cm²

Kết luận:
Diện tích toàn phần của hình trụ là 188,4 cm².

Bài tập ví dụ 2

Bài toán:
Một hình trụ có bán kính đáy r = 5 m, chiều cao h = 10 m. Tính diện tích toàn phần của hình trụ.

Lời giải:
Stp = 2πr h + 2πr²
= 2 × 3,14 × 5 × 10 + 2 × 3,14 × 25
= 314 + 157
= 471 m²

Những lỗi thường gặp khi tính diện tích toàn phần của hình trụ

Nhầm công thức diện tích toàn phần với diện tích xung quanh
Nhiều học sinh chỉ tính 2πr h mà quên cộng diện tích hai mặt đáy.

Quên nhân đôi diện tích đáy
Chỉ tính một mặt đáy thay vì hai mặt đáy của hình trụ.

Sai đơn vị đo
Không đổi bán kính và chiều cao về cùng đơn vị trước khi tính.

Thiếu hoặc sai đơn vị diện tích
Kết quả cuối cùng không ghi hoặc ghi sai đơn vị cm², m²,…

Tính toán nhầm số học
Nhầm lẫn khi nhân với π hoặc bình phương bán kính.

Kết luận

Thông qua bài tập ví dụ và việc nhận diện những lỗi thường gặp, bạn sẽ nắm vững cách tính diện tích toàn phần của hình trụ và tránh được các sai sót không đáng có. Luyện tập thường xuyên sẽ giúp bạn làm bài nhanh và chính xác hơn.