Các công thức tính chu vi hình tam giác dễ hiểu kèm theo bài tập

Chu vi hình tam giác

Chu vi hình tam giác là gì?

Chu vi hình tam giác là tổng độ dài của ba cạnh của hình tam giác. Hình tam giác là một trong những hình dạng cơ bản trong hình học, được xác định bởi ba điểm không thẳng hàng gọi là đỉnh và ba đoạn thẳng nối các đỉnh này lại với nhau, tạo thành các cạnh. Chu vi của hình tam giác không chỉ thể hiện kích thước của hình mà còn là một chỉ số quan trọng trong việc tính toán và thiết kế, đặc biệt trong các lĩnh vực như kiến trúc, kỹ thuật, và xây dựng.

Các công thức tính chu vi hình tam giác 

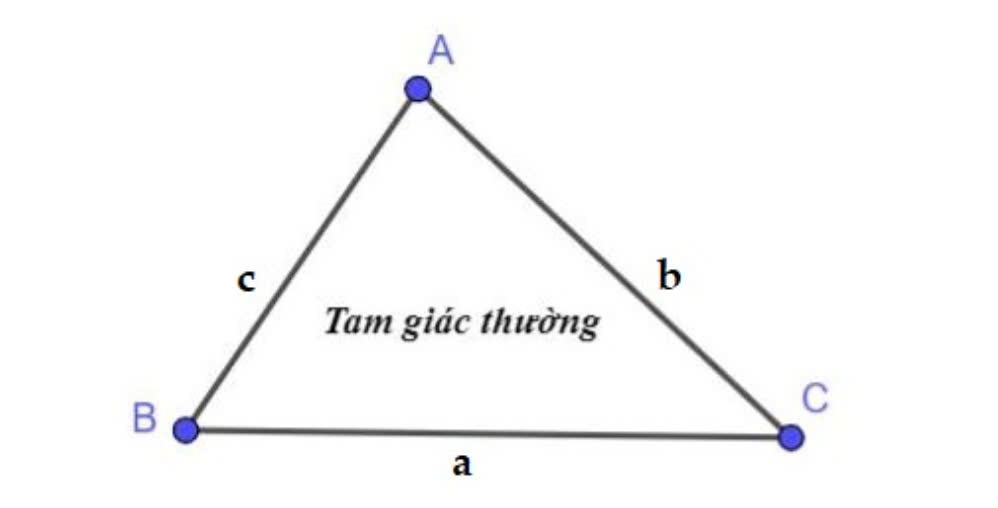
Công thức tính chu vi tam giác thường

Công thức tính chu vi của tam giác thường (hay còn gọi là tam giác bất kỳ) là:

Công thức tính chu vi tam giác:

P=a+b+c

Trong đó:

• P là chu vi của tam giác.
• a, b, và c là độ dài ba cạnh của tam giác.

Ví dụ cụ thể:

Giả sử bạn có một tam giác với các cạnh có độ dài như sau:

• a=5 cm
• b=7 cm
• c=9 cm

Thì chu vi của tam giác sẽ được tính như sau:

P=5+7+9=21 cm

Do vậy để tính chu vi tam giác thường, bạn chỉ cần biết độ dài của ba cạnh và cộng chúng lại với nhau. 

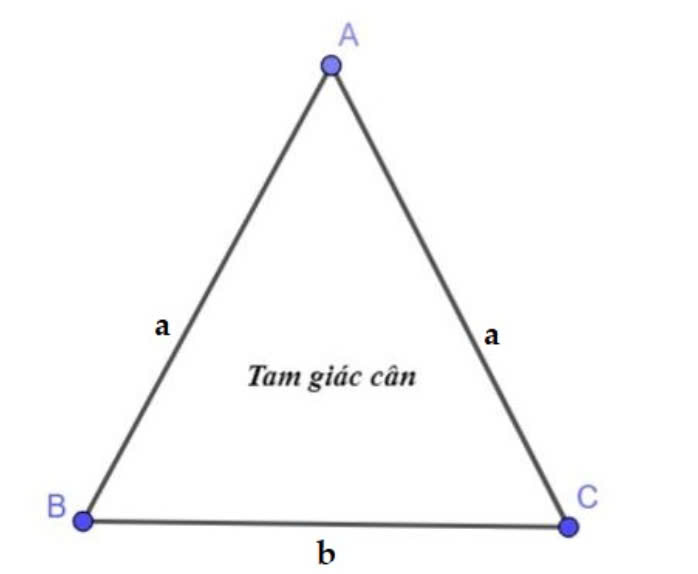
Công thức tính chu vi tam giác cân

Tam giác cân là loại tam giác có hai cạnh bằng nhau. Công thức tính chu vi của tam giác cân được xác định như sau:

Công thức tính chu vi tam giác cân:

P=2a+b

Trong đó:

• Pnlà chu vi của tam giác cân.
• a là độ dài của hai cạnh bằng nhau.
• b là độ dài của cạnh còn lại.

Ví dụ cụ thể:

Giả sử bạn có một tam giác cân với:

• Cạnh bằng nhau a=6 cm
• Cạnh còn lại b=8 cm

Thì chu vi sẽ được tính như sau:

P=2×6+8=12+8=20 cm

Do đó:

Để tính chu vi của tam giác cân, bạn nhân độ dài của cạnh bằng nhau với 2 và sau đó cộng với độ dài của cạnh còn lại. 

Tham khảo: Giá nước ion kiềm

 

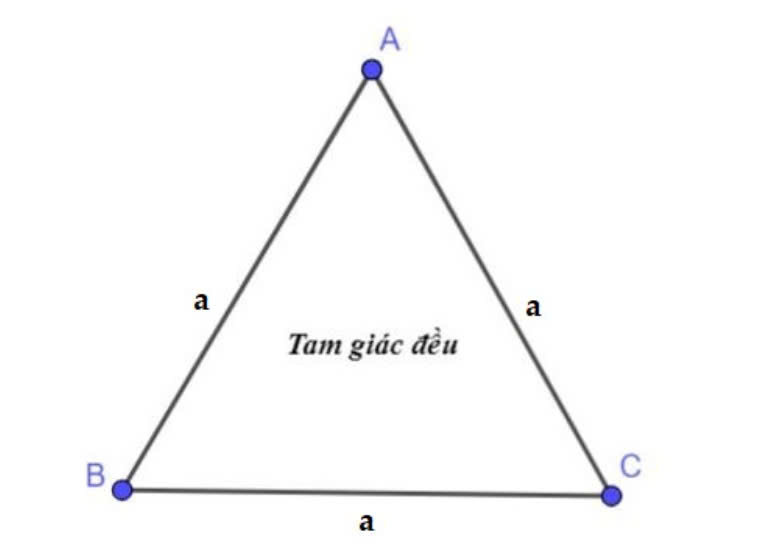
Công thức tính chu vi tam giác đều

Tam giác đều là loại tam giác có ba cạnh bằng nhau. Công thức tính chu vi của tam giác đều được xác định như sau:

Công thức tính chu vi tam giác đều:

P=3a

Trong đó:

• P là chu vi của tam giác đều.
• a là độ dài của một cạnh.

Ví dụ cụ thể:

Giả sử bạn có một tam giác đều với độ dài cạnh là:

• a=5cm

Thì chu vi sẽ được tính như sau:

P=3×5=15 cm

Do vậy: Để tính chu vi của tam giác đều, bạn chỉ cần nhân độ dài của một cạnh với 3. 

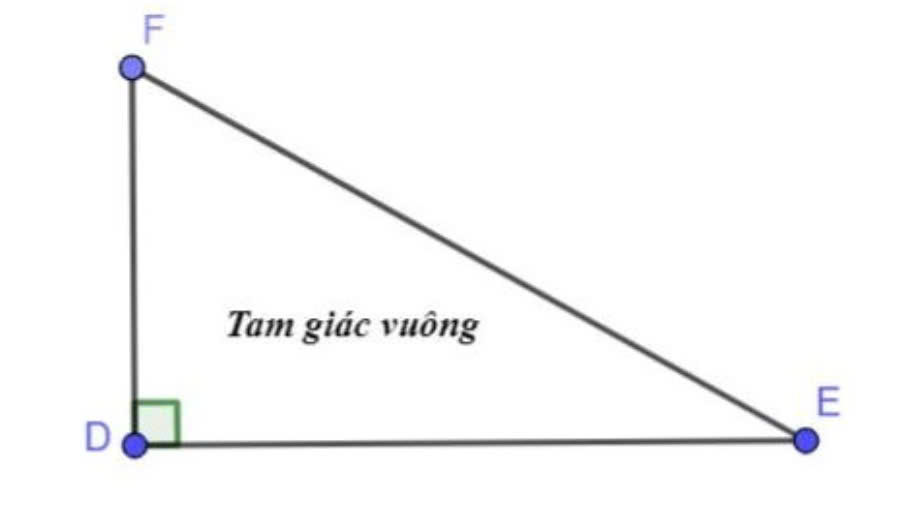
Công thức tính chu vi tam giác vuông

Tam giác vuông là loại tam giác có một góc vuông (90 độ). Công thức tính chu vi của tam giác vuông tương tự như tam giác thường, tức là bạn cần biết độ dài của ba cạnh.

Công thức tính chu vi tam giác vuông:

P=a+b+c

Trong đó:

• P là chu vi của tam giác vuông.
• a và b là độ dài của hai cạnh góc vuông.
• c là độ dài của cạnh huyền.

Ví dụ cụ thể:

Giả sử bạn có một tam giác vuông với:

• Cạnh góc vuông a=3 cm
• Cạnh góc vuông b=4 cm
• Cạnh huyền c=5cm (theo định lý Pythagore: c = √(a² + b²)​)

Thì chu vi sẽ được tính như sau:

P=3+4+5=12 cmP = 3 + 4 + 5 = 12 cm

Do vậy: Để tính chu vi của tam giác vuông, bạn cộng độ dài của hai cạnh góc vuông với độ dài cạnh huyền.

>> Xem thêm: bảng nguyên tố hóa học

Công thức tính chu vi hình tam giác vuông cân

Hình tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. Để tính chu vi của tam giác vuông cân, bạn có thể sử dụng công thức dưới đây.

Công thức tính chu vi của hình tam giác vuông cân:

Giả sử độ dài của hai cạnh góc vuông là aaa (vì nó là tam giác vuông cân, nên hai cạnh này bằng nhau), và cạnh huyền là c.

• Tính cạnh huyền ccc theo định lý Pythagore: c = a√2
• Công thức tính chu vi P: P = a + a + c = 2a + a√2

Ví dụ cụ thể:

Nếu bạn có một tam giác vuông cân với độ dài cạnh góc vuông a=4cm, ta sẽ tính chu vi như sau:

• Tính cạnh huyền: c = 4√2 ≈ 4 * 1.414 = 5.656 cm
• Tính chu vi: P = 2a + c = 2 * 4 + 4 * √2 ≈ 8 + 5.656 ≈ 13.656 cm

>> Xem thêm: Tính diện tích hình chữ nhật

Các dạng bài tập liên quan đến chu vi của hình tam giác 

Dưới đây là một số dạng bài tập liên quan đến chu vi của hình tam giác mà bạn có thể tham khảo:

Bài tập tính chu vi tam giác thường

Dạng bài: Cho độ dài ba cạnh của một tam giác, tính chu vi.

Ví dụ: Tam giác có các cạnh dài 5 cm, 7 cm, và 9 cm. Tính chu vi của tam giác.

Giải:

P=5+7+9=21 cm

Bài tập tính chu vi tam giác cân

Dạng bài: Cho độ dài của một cạnh và yêu cầu tính chu vi của tam giác cân.

Ví dụ: Tam giác cân có cạnh bằng nhau dài 6 cm và cạnh còn lại dài 8 cm. Tính chu vi.

Giải:

P=2×6+8=12+8=20 cm

Bài tập tính chu vi tam giác đều

Dạng bài: Cho độ dài một cạnh của tam giác đều, tính chu vi.

Ví dụ: Tam giác đều có cạnh dài 4 cm. Tính chu vi.

Giải:

P=3×4=12 cm

Bài tập tính chu vi tam giác vuông

Dạng bài: Cho độ dài hai cạnh góc vuông và yêu cầu tính chu vi.

Ví dụ: Tam giác vuông có cạnh góc vuông dài 3 cm và 4 cm. Tính chu vi.

Giải:

• Tính cạnh huyền c: c = √(3² + 4²) = √(9 + 16) = √25 = 5 cm

• Tính chu vi: P=3+4+5=12 cm

Bài tập ứng dụng thực tế

Dạng bài: Một mảnh vườn có hình tam giác. Cho biết độ dài các cạnh của mảnh vườn, tính chu vi để xác định lượng hàng rào cần thiết.

Ví dụ: Một mảnh vườn có các cạnh dài 10 m, 12 m và 14 m. Tính chu vi.

Giải:

P=10+12+14=36 m

Bài tập liên quan đến tính cạnh

Dạng bài: Cho chu vi của tam giác và một số cạnh, yêu cầu tính cạnh còn lại.

Ví dụ: Chu vi tam giác là 30 cm, hai cạnh là 8 cm và 10 cm. Tính cạnh còn lại.

Giải:

P=a+b+c⇒30=8+10+c⇒c=30−18=12 cm

Bài tập tìm độ dài cạnh khi biết chu vi

Dạng bài: Cho chu vi của một tam giác và biết nó là tam giác cân, yêu cầu tính độ dài của một cạnh.

Ví dụ: Tam giác cân có chu vi 24 cm. Tính độ dài một cạnh.

Giải:

P=2a+b⇒24=2a+a⇒24=3a⇒a=8 cm

Các dạng bài tập trên sẽ giúp bạn nắm vững kiến thức về chu vi của hình tam giác và áp dụng vào các bài toán thực tế.

Tính chu vi của hình tam giác là một khái niệm cơ bản nhưng rất quan trọng trong hình học. Qua bài viết, chúng ta đã tìm hiểu về các công thức tính chu vi cho từng loại tam giác, bao gồm tam giác thường, tam giác cân, tam giác đều và tam giác vuông. Mỗi loại hình tam giác có những đặc điểm riêng, và việc nắm vững công thức tính chu vi không chỉ giúp chúng ta giải quyết các bài toán lý thuyết mà còn áp dụng vào thực tiễn trong cuộc sống hàng ngày.

Chu vi của hình tam giác không chỉ là tổng độ dài các cạnh mà còn là nền tảng cho nhiều ứng dụng trong thiết kế, xây dựng và nghệ thuật. Hiểu rõ về chu vi của tam giác sẽ giúp chúng ta phát triển tư duy logic và khả năng giải quyết vấn đề, góp phần vào việc học tập và nghiên cứu các lĩnh vực khác trong toán học và khoa học. Hy vọng rằng bài viết này đã mang lại cho bạn những kiến thức hữu ích và thú vị về chu vi của hình tam giác.

Đừng quên theo dõi NỘI THẤT HOÀNG GIA để cập nhật những mẫu thiết kế nội thất hiện đại mỗi ngày nhé!

>> Tham khảo: Mẫu tủ bếp gỗ tự nhiên hiện đại