Chu vi hình tam giác – Công thức, ví dụ chi tiết và ứng dụng thực tế

Chu vi hình tam giác là gì, cách tính ra sao? Tìm hiểu công thức tính chu vi tam giác đều, vuông, cân và thường, kèm ví dụ minh họa, ứng dụng trong học tập, kiến trúc, và mẹo ghi nhớ dễ hiểu cho học sinh.

Chu vi hình tam giác

Hiểu rõ khái niệm chu vi hình tam giác

Khái niệm cơ bản

Hình tam giác là một trong những hình học cơ bản nhất trong toán học, được tạo bởi ba đoạn thẳng nối ba điểm không thẳng hàng. Mỗi tam giác có ba cạnh, ba góc và ba đỉnh. Đây là hình xuất hiện rất sớm trong các bài học hình học vì nó mang nhiều tính chất thú vị và có tính ứng dụng cao trong đời sống, kiến trúc và kỹ thuật.

Chu vi hình tam giác là độ dài đường bao quanh tam giác, tức là tổng độ dài của ba cạnh. Khi bạn đi quanh một khu vườn, một tấm bảng hoặc một khung cửa hình tam giác, quãng đường bạn đi chính là chu vi của tam giác đó. Chu vi thường được ký hiệu là P, đơn vị đo có thể là cm, m, km hoặc bất kỳ đơn vị độ dài nào tương ứng với kích thước hình.

Trong thực tế, việc hiểu và tính đúng chu vi rất quan trọng. Khi cần may một tấm vải hình tam giác, thiết kế khung kim loại, hoặc đo vật liệu bao quanh công trình, việc biết chu vi giúp bạn ước lượng chính xác lượng vật liệu cần dùng, tránh lãng phí.

Tính chất liên quan đến chu vi

Chu vi tam giác không chỉ thể hiện tổng độ dài ba cạnh mà còn liên quan mật thiết đến diện tích, tỷ lệ cạnh, góc, và hình dạng tam giác. Nếu hai tam giác có tỷ lệ chu vi bằng nhau thì các cạnh của chúng cũng tỉ lệ thuận với nhau – đây là nền tảng của khái niệm tam giác đồng dạng trong hình học.

Hình tam giác

Công thức tính chu vi hình tam giác và các dạng đặc biệt

Công thức tổng quát

Với mọi tam giác, dù là đều, vuông hay cân, công thức tính chu vi đều xuất phát từ nguyên lý cơ bản: chu vi bằng tổng độ dài ba cạnh. Nếu ba cạnh có độ dài lần lượt là a, b và c, ta có:

P = a + b + c

Công thức này đơn giản nhưng bao quát mọi trường hợp. Trong hình học phẳng, chỉ cần biết độ dài các cạnh, bạn có thể nhanh chóng tính được chu vi.

Chu vi tam giác đều

Tam giác đều là loại tam giác có ba cạnh bằng nhau và ba góc đều bằng 60 độ. Khi đó, chu vi được rút gọn thành công thức ngắn gọn:

P = 3 × a, trong đó a là độ dài cạnh.

Chu vi tam giác vuông

Tam giác vuông có một góc 90 độ, thường được ký hiệu với hai cạnh góc vuông là a và b, cạnh huyền là c. Công thức tính chu vi vẫn là P = a + b + c. Tuy nhiên, trong nhiều bài toán, bạn không biết cạnh huyền mà chỉ biết hai cạnh góc vuông. Khi đó, bạn cần áp dụng định lý Pythagoras để tìm cạnh còn lại:

c = √(a² + b²)

Từ đó, chu vi là P = a + b + √(a² + b²).

Chẳng hạn, một tam giác vuông có hai cạnh góc vuông lần lượt là 9 cm và 12 cm. Khi đó, cạnh huyền là √(9² + 12²) = √(81 + 144) = √225 = 15 cm. Chu vi tam giác này sẽ là P = 9 + 12 + 15 = 36 cm.

Chu vi tam giác cân và tam giác thường

Tam giác cân có hai cạnh bằng nhau, vì thế công thức tính chu vi là P = 2a + c, trong đó a là cạnh bên và c là cạnh đáy. Nếu tam giác có hai cạnh bên dài 10 cm và cạnh đáy dài 12 cm, thì P = 2 × 10 + 12 = 32 cm.

Với tam giác thường, tức là ba cạnh khác nhau, công thức tổng quát P = a + b + c vẫn được áp dụng. Điểm quan trọng khi tính chu vi loại tam giác này là cần đo chính xác từng cạnh. Trong kiến trúc hoặc thiết kế, việc đo sai chỉ 1 cm có thể khiến tam giác không khép kín, gây sai lệch toàn bộ kết cấu.

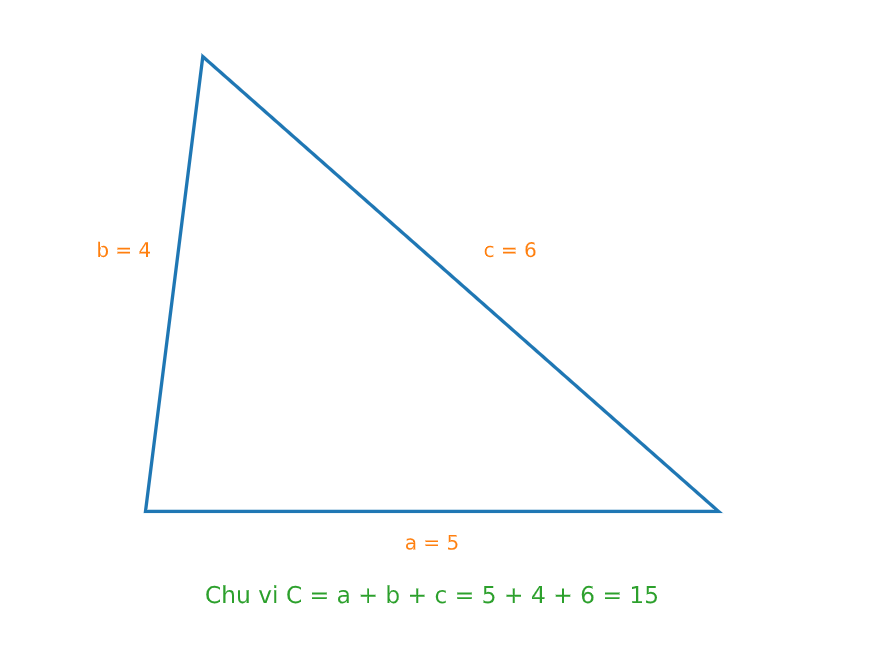
Chu vi tam giác

Tính chu vi tam giác trong hệ tọa độ và các tình huống đặc biệt

Trong toán học hiện đại, tam giác có thể được biểu diễn trong hệ tọa độ Oxy bằng ba điểm A(x₁, y₁), B(x₂, y₂), và C(x₃, y₃). Khi đó, độ dài mỗi cạnh được tính bằng công thức khoảng cách giữa hai điểm trong mặt phẳng:

AB = √((x₂ – x₁)² + (y₂ – y₁)²)
BC = √((x₃ – x₂)² + (y₃ – y₂)²)
CA = √((x₁ – x₃)² + (y₁ – y₃)²)

Sau khi tính được ba cạnh, chỉ cần cộng lại để ra chu vi P = AB + BC + CA.

Ví dụ, tam giác có tọa độ A(0, 0), B(4, 0) và C(0, 3). Khi đó, AB = 4, AC = 3, BC = √(4² + 3²) = 5. Vậy chu vi tam giác là P = 4 + 3 + 5 = 12 đơn vị độ dài.

Trường hợp khác, nếu biết hai cạnh và góc xen giữa, bạn có thể dùng định lý cos để tìm cạnh còn lại:
c² = a² + b² – 2ab × cos(C).
Sau khi tính ra cạnh c, chu vi sẽ bằng a + b + c. Cách này thường được dùng trong các bài toán lượng giác hoặc khi đo thực địa bằng công cụ góc, như trong trắc địa hoặc kiến trúc.

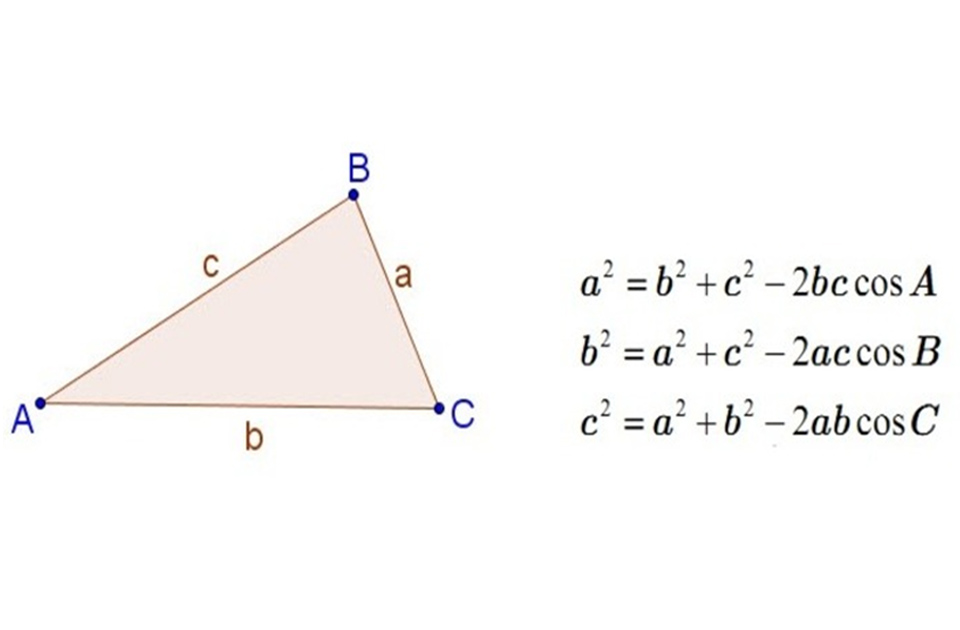
Định lý cos

Ứng dụng công thức chu vi tam giác trong đời sống và kỹ thuật

Công thức chu vi hình tam giác không chỉ tồn tại trong sách giáo khoa mà còn được ứng dụng rộng rãi trong nhiều lĩnh vực. Trong kiến trúc, tam giác được xem là hình học vững chắc nhất vì nó phân bố đều lực tại ba điểm. Khi thiết kế mái nhà, cầu trục hoặc khung sắt, kỹ sư cần biết chính xác chu vi của các tam giác cấu thành để cắt vật liệu đúng kích thước.

Trong lĩnh vực chế tạo, chu vi giúp xác định chiều dài khung viền, dây cáp, mép vật liệu cần bao quanh sản phẩm. Một chiếc khung cửa sổ tam giác hay tấm gương trang trí, dù nhỏ, cũng cần tính chu vi chính xác để thi công vừa khít.

Với học sinh, hiểu rõ chu vi tam giác giúp các em làm quen với tư duy đo lường, tính toán thực tế và hình dung được mối liên hệ giữa các đại lượng hình học. Đây cũng là nền tảng để học các khái niệm nâng cao hơn như chu vi đa giác, diện tích hình phẳng và tỉ số đồng dạng.

Chu vi hình tam giác là khái niệm cơ bản nhưng vô cùng quan trọng, không chỉ trong học tập mà còn trong thực tế đời sống và kỹ thuật. Công thức P = a + b + c tuy đơn giản nhưng giúp giải quyết nhiều bài toán khác nhau, từ thiết kế, xây dựng cho đến đo đạc vật liệu.