Chu Vi Hình Tam Giác Là Gì? Cách Tính, Ứng Dụng Dễ Hiểu Cho Mọi Người

Tìm hiểu chu vi hình tam giác là gì, cách tính cho các loại tam giác và ứng dụng thực tế. Giải thích đơn giản, dễ nhớ, giúp bạn áp dụng chính xác ngay lập tức.

Khái niệm chu vi hình tam giác và ý nghĩa trong thực tế

Chu vi hình tam giác là gì?

Chu vi hình tam giác là tổng độ dài ba cạnh tạo nên hình tam giác. Đây là một khái niệm cơ bản nhưng đóng vai trò rất quan trọng trong toán học và thực tế. Khi bạn biết độ dài của từng cạnh, bạn chỉ cần cộng lại để tìm được chu vi. Đây là bước đầu tiên trong việc tính diện tích, tính chiều dài rào chắn, hay dự toán nguyên vật liệu xây dựng.

Trong toán học, khái niệm chu vi giúp bạn làm quen với các yếu tố hình học, từ đó phát triển tư duy về đo lường, không gian và tính chính xác. Khi học về chu vi tam giác, bạn không chỉ học cách cộng ba số lại với nhau, mà còn học cách quan sát và phân tích hình dáng của một đối tượng trong không gian hai chiều.

Tại sao phải quan tâm đến chu vi?

Việc biết chu vi tam giác có thể giúp bạn giải quyết nhiều vấn đề thực tế. Nếu bạn muốn dựng hàng rào quanh một mảnh đất hình tam giác, bạn phải biết chu vi để tính được chiều dài dây cần dùng. Nếu bạn làm thủ công mỹ nghệ như gấp giấy, làm mô hình hoặc thiết kế kỹ thuật, việc đo và xác định chu vi cũng là bước đầu tiên cần thực hiện chính xác.

Không chỉ vậy, chu vi còn được dùng để xác định giới hạn của vùng bao quanh, từ đó phục vụ các bài toán tối ưu hoá như tìm diện tích lớn nhất với chu vi cố định, hoặc tìm cách sử dụng nguyên liệu tiết kiệm nhất.

Tam giác đều với chu vi bằng ba lần cạnh

Cách tính chu vi tam giác đơn giản và dễ nhớ

Công thức cơ bản

Chu vi tam giác được tính bằng cách cộng độ dài của ba cạnh. Công thức tổng quát như sau:

Chu vi = a + b + c

Trong đó a, b, c lần lượt là độ dài các cạnh của tam giác. Dù tam giác có dạng gì đi nữa – đều, cân hay thường – bạn vẫn có thể áp dụng công thức này miễn là biết được độ dài của ba cạnh.

Giả sử bạn có một tam giác với các cạnh lần lượt là 5 cm, 7 cm và 8 cm. Khi đó chu vi sẽ là 5 + 7 + 8 = 20 cm. Cách tính rất đơn giản, nhưng điều quan trọng là bạn phải chắc chắn rằng số liệu về các cạnh là chính xác.

Những lưu ý khi tính chu vi

Một điều bạn cần lưu ý là chu vi không phụ thuộc vào diện tích hay góc của tam giác. Chỉ cần bạn biết được ba cạnh thì dù tam giác nhọn, vuông hay tù, công thức vẫn không thay đổi. Nếu chỉ biết một hoặc hai cạnh, bạn sẽ cần thêm thông tin bổ sung, chẳng hạn như góc hoặc chiều cao, để tính được cạnh còn lại.

Trong một số trường hợp đặc biệt như tam giác đều, bạn có thể sử dụng cách tính nhanh hơn. Nếu biết cạnh là a, thì chu vi là 3a. Nhưng dù cách tính có thể khác nhau ở từng loại tam giác, thì bản chất vẫn là tổng độ dài các cạnh.

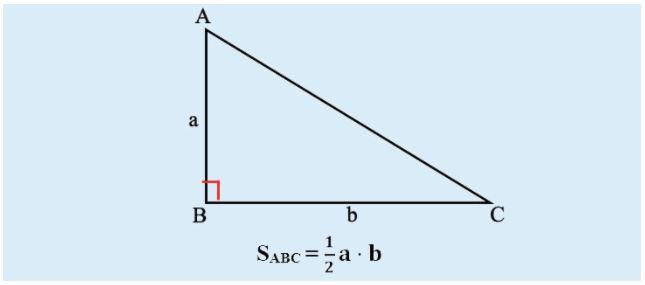
Tính chu vi của tam giác vuông

Phân loại và công thức chu vi theo từng dạng tam giác

Tam giác đều

Tam giác đều có ba cạnh bằng nhau, vì vậy bạn chỉ cần biết một cạnh duy nhất. Khi đó, chu vi được tính theo công thức:

Chu vi = 3 * a

Với cạnh a bằng 6 cm, chu vi sẽ là 18 cm. Cách tính này cực kỳ nhanh và được áp dụng nhiều trong hình học cơ bản cũng như các bài toán mô hình đều.

Tam giác cân

Tam giác cân có hai cạnh bên bằng nhau và một đáy khác. Nếu gọi hai cạnh bằng nhau là a và đáy là b, công thức sẽ là:

Chu vi = 2 * a + b

Trong trường hợp bạn biết độ dài của hai cạnh bên là 5 cm và cạnh đáy là 6 cm, chu vi sẽ là 2 * 5 + 6 = 16 cm.

Tam giác vuông

Tam giác vuông có một góc 90 độ và thường được áp dụng định lý Pythagoras để tìm cạnh còn thiếu nếu chưa đủ dữ kiện. Sau khi có đủ ba cạnh, bạn vẫn tính chu vi bằng công thức tổng ba cạnh.

Ví dụ, với tam giác vuông có hai cạnh góc vuông là 3 cm và 4 cm, cạnh huyền sẽ là 5 cm. Khi đó chu vi là 3 + 4 + 5 = 12 cm. Đây là một ví dụ kinh điển thường được dùng trong toán học lớp dưới để làm quen với khái niệm chu vi.

Chu vi tam giác được dùng để tính chiều dài rào trong thực tế

Ứng dụng của chu vi tam giác trong đời sống

Trong xây dựng và thiết kế

Một trong những ứng dụng thực tế dễ thấy nhất của chu vi hình tam giác là trong lĩnh vực xây dựng. Khi đo đạc đất đai, bạn có thể gặp những mảnh đất có hình tam giác. Biết được chu vi sẽ giúp bạn xác định được chiều dài rào, số lượng vật liệu cần dùng như sắt, thép hoặc xi măng. Việc tính đúng chu vi giúp tiết kiệm chi phí và đảm bảo chính xác trong thi công.

Trong thiết kế nội thất hay kiến trúc, chu vi cũng là cơ sở để xác định kích thước các khối hình học, từ đó bố trí hợp lý không gian trong phòng hoặc toàn bộ công trình. Đặc biệt với những thiết kế mang yếu tố hình học, việc tính chu vi và diện tích là bước không thể thiếu.

Trong đời sống và học tập

Ngoài lĩnh vực xây dựng, chu vi tam giác còn rất quen thuộc trong các hoạt động đời thường. Khi may quần áo, làm thủ công, hoặc thậm chí cắt giấy, bạn cũng sẽ gặp hình tam giác và cần tính chu vi để cắt, dán chính xác. Việc hiểu rõ cách tính chu vi sẽ giúp bạn tự tin hơn khi làm việc thực hành, tiết kiệm thời gian và hạn chế sai sót.

Trong học tập, đặc biệt ở các cấp học phổ thông, bài toán về chu vi tam giác giúp học sinh làm quen với tư duy không gian và kỹ năng tính toán chính xác. Đây là nền tảng để học sinh phát triển các kỹ năng giải bài toán phức tạp hơn sau này.

Chu vi hình tam giác không chỉ là một kiến thức toán học cơ bản mà còn là công cụ hữu ích trong rất nhiều tình huống thực tế. Dù bạn là học sinh, người lao động, kỹ sư hay chỉ đơn giản là người yêu thích tính toán, việc nắm rõ khái niệm và công thức chu vi sẽ giúp bạn làm việc hiệu quả và chính xác hơn. Hãy luyện tập thường xuyên để ghi nhớ và vận dụng thành thạo kiến thức này trong mọi lĩnh vực của cuộc sống.