Diện Tích Xung Quanh Hình Nón – Cách Tính, Giải Thích Và Ứng Dụng

Tìm hiểu công thức tính diện tích xung quanh hình nón, giải thích chi tiết, ví dụ minh họa và ứng dụng thực tế giúp bạn hiểu sâu, ghi nhớ lâu và vận dụng dễ dàng trong học tập cũng như đời sống.

Diện tích xung quanh hình nón​

Hình nón và các yếu tố cấu tạo

Trong hình học không gian, hình nón là một khối tròn xoay quen thuộc, xuất hiện khắp nơi quanh ta: từ chiếc mũ lá, cái phễu, đến ốc quế kem. Khi học về hình nón, kiến thức quan trọng nhất mà bất kỳ học sinh nào cũng cần nắm chính là diện tích xung quanh hình nón. Đây là phần diện tích bao quanh mặt cong của hình nón – phần được tạo ra khi tam giác vuông quay quanh một cạnh góc vuông.

Khái niệm về hình nón

Hình nón là hình khối được tạo ra khi một tam giác vuông quay quanh một cạnh góc vuông cố định. Khi đó, cạnh còn lại của tam giác tạo thành mặt cong, và cạnh quay làm trục đối xứng của hình nón.

Hình nón bao gồm hai phần chính: phần mặt cong gọi là mặt xung quanh, và phần đáy là một hình tròn. Mặt cong này chính là vùng chúng ta cần tính diện tích xung quanh.

Các yếu tố cơ bản

Một hình nón có ba yếu tố quan trọng gồm bán kính đáy (r), chiều cao (h) và đường sinh (l). Bán kính đáy là khoảng cách từ tâm đến mép của hình tròn đáy. Chiều cao là đoạn thẳng vuông góc từ đỉnh nón xuống tâm đáy. Đường sinh là đoạn nối đỉnh nón với một điểm bất kỳ trên chu vi đáy. Ba yếu tố này liên hệ với nhau qua công thức Pythagoras: l² = r² + h².

Hình nón

Công thức tính diện tích xung quanh của hình nón

Định nghĩa

Diện tích xung quanh hình nón là phần diện tích của mặt cong bao quanh khối nón, không tính phần đáy. Nếu bạn tưởng tượng “mở phẳng” phần mặt cong này ra, bạn sẽ thu được một hình quạt tròn có bán kính bằng đường sinh (l) và độ dài cung tròn bằng chu vi đáy (2πr).

Công thức chuẩn

Từ đó, ta suy ra công thức diện tích xung quanh của hình nón là:

Sxq = π × r × l

Trong đó:

Sxq là diện tích xung quanh hình nón.

r là bán kính đáy.

l là đường sinh.

π (pi) là hằng số, lấy xấp xỉ 3,14.

Giải thích ý nghĩa

Nếu hình quạt tròn có bán kính l và cung tròn là 2πr, thì diện tích hình quạt sẽ bằng (cung tròn × bán kính) / 2. Thay giá trị vào ta được:
S = (2πr × l) / 2 = πrl.
Như vậy, công thức diện tích xung quanh hình nón thực chất là diện tích của hình quạt tròn được “mở ra” từ mặt cong của hình nón.

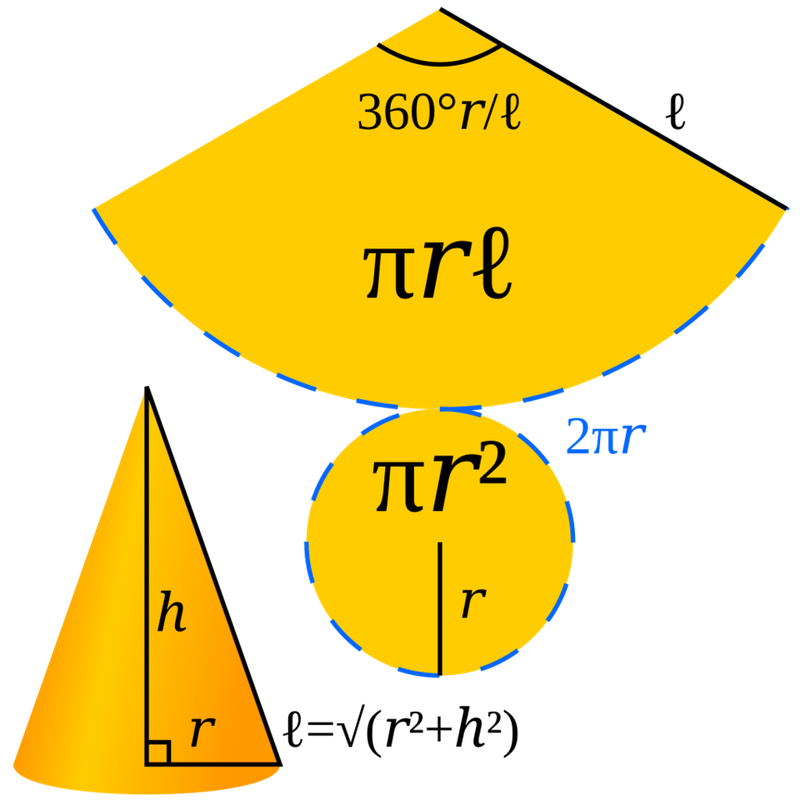
Diện tích của hình nón

Các công thức liên quan đến hình nón

Diện tích toàn phần

Diện tích toàn phần của hình nón bao gồm cả phần mặt đáy, được tính bằng công thức:
Stp = Sxq + Sđáy = πrl + πr² = πr(l + r).

Thể tích hình nón

Ngoài diện tích, hình nón còn có thể tích được tính bằng công thức:
V = (1/3) × πr²h.
Thể tích cho biết không gian mà khối nón chiếm, còn diện tích phản ánh phần bề mặt bao quanh nó.

Mối liên hệ giữa các đại lượng

Khi biết hai trong ba giá trị r, h, l, bạn có thể dễ dàng tìm được đại lượng còn lại nhờ công thức Pythagoras. Nhờ đó, các công thức diện tích và thể tích có thể được áp dụng linh hoạt trong nhiều dạng bài toán khác nhau.

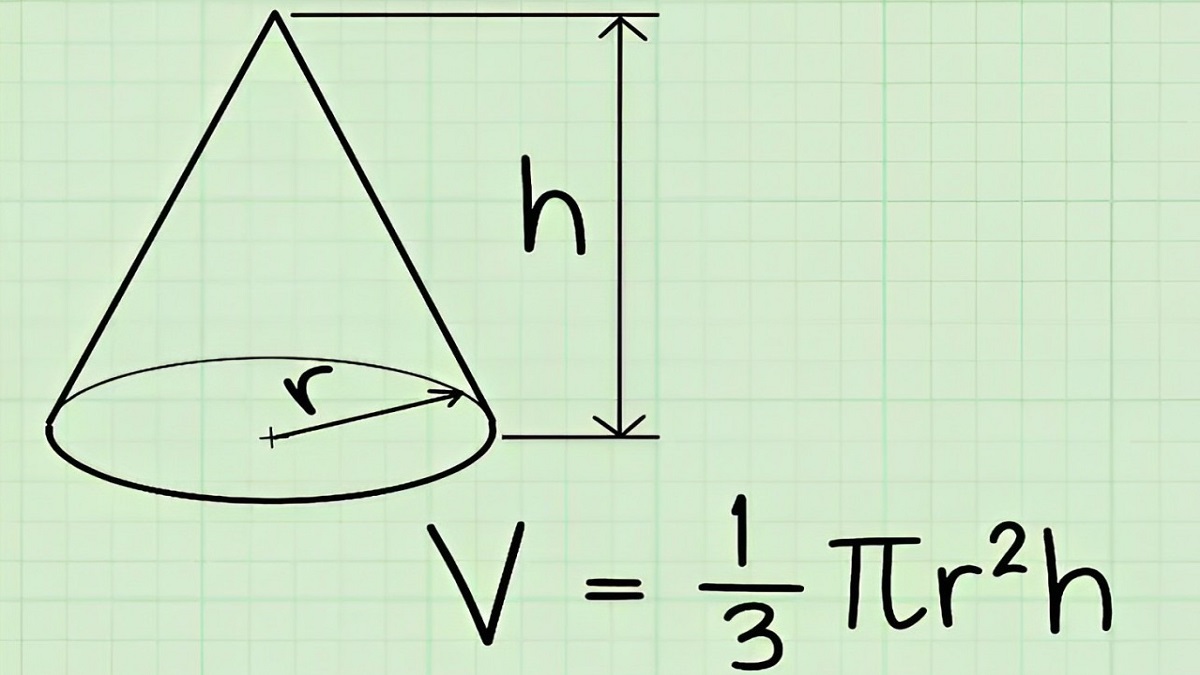
Thể tích hình nón

Ví dụ minh họa cách tính diện tích xung quanh

Ví dụ 1

Một hình nón có bán kính đáy r = 5 cm và đường sinh l = 13 cm.
Áp dụng công thức: Sxq = πrl = 3,14 × 5 × 13 = 204,1 cm².
Kết luận: Diện tích xung quanh hình nón là 204,1 cm².

Ví dụ 2

Một hình nón khác có chiều cao h = 12 cm và bán kính đáy r = 9 cm. Trước tiên, tính đường sinh l bằng định lý Pythagoras:
l² = r² + h² = 9² + 12² = 225 → l = 15 cm.
Khi đó, Sxq = πrl = 3,14 × 9 × 15 = 424,65 cm².
Kết luận: Diện tích xung quanh hình nón là 424,65 cm².

Qua hai ví dụ trên, có thể thấy việc nắm vững mối quan hệ giữa r, h và l giúp bạn tính toán nhanh chóng và chính xác hơn.

Ứng dụng của công thức diện tích xung quanh của hình nón

Công thức Sxq = πrl có rất nhiều ứng dụng thực tế trong đời sống. Khi chế tạo hoặc thiết kế các vật có dạng hình nón như mũ, phễu, ống khói, mái chóp hay ốc quế, người ta cần biết diện tích xung quanh để ước lượng lượng vật liệu cần sử dụng.

Trong kiến trúc, công thức này giúp kỹ sư tính toán phần mái vòm hoặc tháp tròn có dạng hình nón. Còn trong lĩnh vực mỹ thuật hay thiết kế sản phẩm, công thức này giúp người làm có thể tạo ra mô hình chính xác về kích thước và tỷ lệ.

Với học sinh, việc hiểu bản chất công thức giúp phát triển tư duy hình học không gian. Khi nhận ra rằng mặt xung quanh hình nón là một phần của hình tròn, bạn sẽ dễ dàng ghi nhớ và vận dụng công thức vào những bài toán tổng hợp, thay vì chỉ học thuộc lòng.

Những sai lầm thường gặp khi tính diện tích hình nón

Một sai lầm phổ biến là nhầm lẫn giữa chiều cao (h) và đường sinh (l). Nhiều bạn áp dụng sai đại lượng, dẫn đến kết quả không chính xác. Cần nhớ rằng l luôn lớn hơn h và được tính bằng công thức l² = r² + h².

Một lỗi khác là quên cộng diện tích đáy khi đề bài yêu cầu diện tích toàn phần thay vì diện tích xung quanh. Ngoài ra, nhiều người còn mắc lỗi không thống nhất đơn vị đo giữa r, h và l. Nếu một đại lượng tính bằng cm và đại lượng khác tính bằng m, kết quả sẽ sai lệch đáng kể.

Diện tích xung quanh của hình nón là phần diện tích mặt cong bao quanh khối nón, được tính theo công thức Sxq = πrl. Đây là một trong những công thức cơ bản nhất của hình học không gian, giúp xác định phần bề mặt của hình nón trong học tập cũng như trong thực tế.

Việc hiểu rõ nguồn gốc và ý nghĩa của công thức giúp bạn không còn học thuộc máy móc, mà có thể nhìn thấy sự liên kết giữa các yếu tố hình học. Khi đó, mỗi bài toán hình nón không chỉ là một phép tính, mà còn là cách để bạn khám phá sự hài hòa giữa toán học và thực tế – nơi mọi con số đều mang một hình dạng, một câu chuyện và một ý nghĩa riêng.