Hình nón là gì? Công thức tính diện tích xung quanh hình nón​

Diện tích xung quanh hình nón​

Hình nón là gì

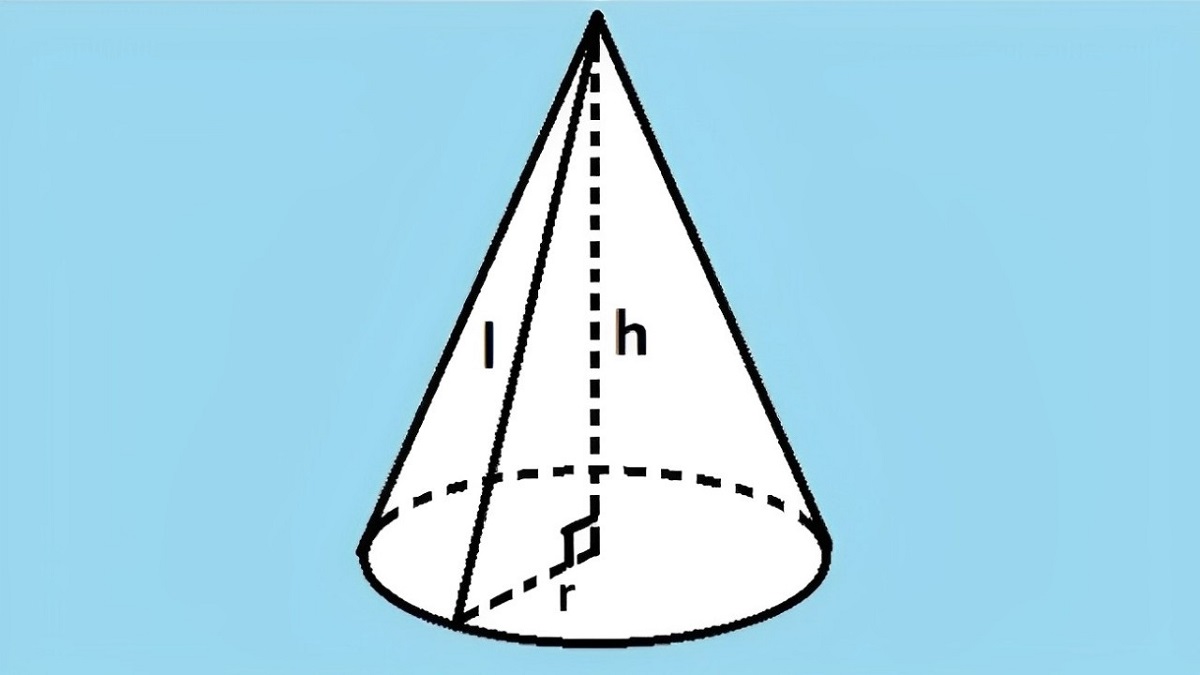
Hình nón là một khối hình học ba chiều được tạo thành từ một đáy là hình tròn và một đỉnh duy nhất, nơi tất cả các đường thẳng nối từ đỉnh đến các điểm trên đường tròn đáy tạo thành một bề mặt cong. Dưới đây là mô tả chi tiết về hình nón:

Đặc điểm của hình nón

• Đỉnh: Là điểm cao nhất hoặc chóp của hình nón, không nằm trên mặt đáy.
• Đáy: Là hình tròn, nằm ở mặt phẳng đáy của hình nón.
• Đường sinh: Là đoạn thẳng nối từ đỉnh đến một điểm bất kỳ trên đường tròn đáy.
• Chiều cao (h): Là khoảng cách vuông góc từ đỉnh đến tâm của đáy.
• Bán kính đáy (r): Là khoảng cách từ tâm của đáy đến bất kỳ điểm nào trên đường tròn đáy.

Phân loại hình nón

• Hình nón tròn đều: Là hình nón có đáy là một hình tròn và đỉnh nằm trên trục đối xứng của đáy.
• Hình nón xiên: Là hình nón có đỉnh không nằm trên trục đối xứng của đáy.
• Hình nón cụt: Là phần còn lại của hình nón khi đỉnh bị cắt đi bởi một mặt phẳng song song với đáy.

Khi nào cần dùng diện tích xung quanh của hình nón?

Diện tích xung quanh của hình nón được sử dụng khi chỉ cần tính diện tích của phần mặt cong bên ngoài, không bao gồm đáy của hình nón. Dưới đây là các tình huống cụ thể khi cần dùng đến diện tích xung quanh hình nón:

Tính toán vật liệu bọc hoặc sơn

• Khi cần xác định diện tích vật liệu cần dùng để bọc, sơn, hoặc phủ lên phần mặt cong của hình nón:
  • Ví dụ: Tính lượng giấy để bọc một chiếc nón giấy hoặc lượng sơn cần dùng để sơn mặt ngoài của một phễu hình nón.

Tính bề mặt tiếp xúc

• Khi cần tính diện tích bề mặt tiếp xúc bên ngoài của hình nón, chẳng hạn trong thiết kế kỹ thuật hoặc sản xuất.
  • Ví dụ: Tính bề mặt tiếp xúc của một nón chắn gió trên xe ô tô.

Thiết kế và trang trí

• Khi làm các sản phẩm hình nón như nón lễ hội, phễu, hoặc trang trí, diện tích xung quanh giúp xác định kích thước và mẫu thiết kế:
  • Ví dụ: Tính diện tích giấy cần để in mẫu hoa văn cho một chiếc nón giấy.

Ứng dụng trong kiến trúc

• Trong thiết kế các công trình có phần mái dạng hình nón (như lều, mái đình), cần tính diện tích xung quanh để dự trù vật liệu.
  • Ví dụ: Tính diện tích tấm lợp cần để che một mái hình nón.

Tính toán công suất hoặc hiệu quả

• Trong vật lý hoặc kỹ thuật, khi bề mặt cong của hình nón tham gia vào quá trình dẫn nhiệt, phát sáng, hoặc phản chiếu, diện tích xung quanh đóng vai trò quan trọng.
  • Ví dụ: Tính bề mặt phát sáng của một đèn hình nón.

Sử dụng trong học tập

• Khi giải các bài tập hình học liên quan đến diện tích xung quanh của hình nón để rèn luyện khả năng tính toán và áp dụng công thức:
  • Ví dụ: Một bài toán yêu cầu chỉ tính phần diện tích cong của hình nón mà không cần đến diện tích đáy.

Khi làm mô hình hoặc sản phẩm thực tế

• Khi cần làm các mô hình hình nón từ giấy hoặc vật liệu khác, diện tích xung quanh giúp tính toán kích thước vật liệu cần dùng.
  • Ví dụ: Cắt một tấm giấy có diện tích đúng bằng diện tích xung quanh để gấp thành hình nón.

Diện tích xung quanh của hình nón được dùng khi chỉ cần tính toán phần mặt cong bên ngoài mà không liên quan đến đáy. Đây là thông số quan trọng trong sản xuất, thiết kế, học tập, và các ứng dụng thực tế liên quan đến hình học không gian.

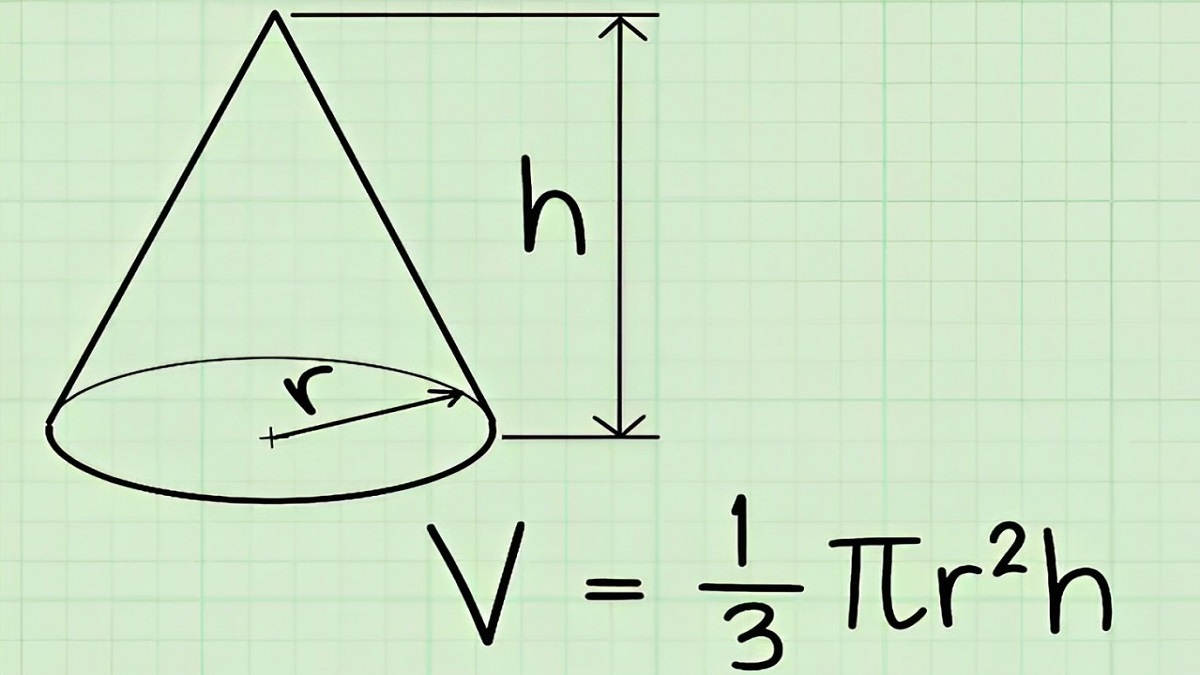
Các công thức tính diện tích xung quanh hình nón​

Thể tích:
V = 1/3 * π * r² * h
Trong đó:

• r: Bán kính đáy.
• h: Chiều cao của hình nón.

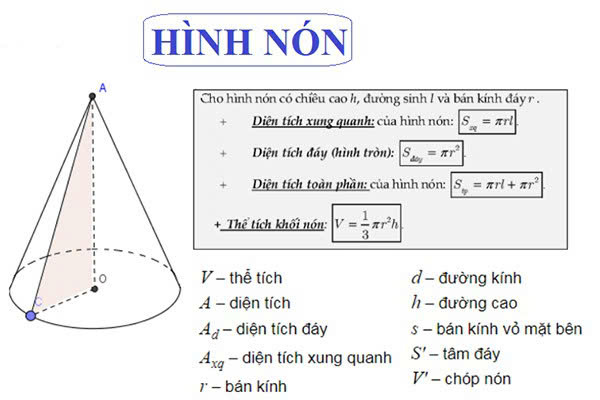
Diện tích xung quanh:
Aₓ = π * r * l
Trong đó:

• r: Bán kính đáy.
• l: Đường sinh.

Diện tích toàn phần:
Aₜ = π * r * l + π * r²

• Bao gồm diện tích xung quanh và diện tích đáy.

Ứng dụng thực tế của diện tích xung quanh hình nón là gì?

Diện tích xung quanh của hình nón có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng thực tế của diện tích xung quanh hình nón:

Thiết kế và sản xuất nón (giấy, nhựa, vải)

• Ví dụ: Khi làm nón giấy, nón lá, nón bảo hiểm hoặc các loại nón khác, cần tính diện tích xung quanh để xác định lượng vật liệu cần sử dụng. Diện tích xung quanh giúp tính toán chính xác lượng giấy, vải hoặc nhựa cần cắt để tạo hình nón.

Làm phễu (funnel)

• Ví dụ: Các phễu dùng để đổ chất lỏng hoặc bột từ một bình chứa lớn vào bình chứa nhỏ hơn thường có dạng hình nón. Diện tích xung quanh giúp xác định kích thước của phễu, từ đó tính toán lượng vật liệu cần làm phễu.

Xây dựng mái nhà hình nón

• Ví dụ: Một số công trình kiến trúc sử dụng mái nhà có dạng hình nón (chẳng hạn như các mái vòm của nhà thờ, lều trại, hoặc các công trình mang tính biểu tượng). Diện tích xung quanh của hình nón giúp xác định diện tích tấm lợp cần thiết để phủ mái.

Trang trí và thiết kế đồ vật

• Ví dụ: Trong nghệ thuật trang trí, thiết kế sản phẩm (như đèn trang trí, chậu cây), hình nón được sử dụng để tạo ra các sản phẩm có hình dạng đẹp mắt. Diện tích xung quanh giúp xác định độ lớn và vật liệu cần thiết để sản xuất các đồ vật này.

Thiết kế vỏ tên lửa hoặc động cơ tên lửa

• Ví dụ: Các bộ phận của tên lửa như đầu mũi hoặc động cơ có thể có dạng hình nón. Diện tích xung quanh giúp tính toán vật liệu chế tạo và tính toán khí động học, độ bền của các bộ phận này.

Tính toán diện tích sơn hoặc phủ bề mặt

• Ví dụ: Khi cần phủ một lớp sơn lên bề mặt cong của hình nón, diện tích xung quanh sẽ cho biết diện tích bề mặt cần sơn. Điều này rất quan trọng trong ngành xây dựng và sản xuất để tính toán chi phí và lượng sơn cần dùng.

Ứng dụng trong các thiết bị âm thanh

• Ví dụ: Một số loa và thiết bị âm thanh có dạng hình nón. Diện tích xung quanh có thể giúp tính toán hiệu quả khuếch tán âm thanh hoặc vật liệu cần thiết để làm loa.

Tính toán diện tích vật liệu trong sản xuất công nghiệp

• Ví dụ: Trong các ngành công nghiệp như sản xuất ống dẫn, phễu, hay các thiết bị chứa chất lỏng, diện tích xung quanh giúp tính toán kích thước và vật liệu cần sử dụng để chế tạo các sản phẩm này.

Tính toán thể tích chất lỏng trong phễu hình nón

• Ví dụ: Phễu hình nón thường được dùng trong các phòng thí nghiệm hoặc nhà máy để chuyển chất lỏng từ bể chứa lớn sang bình chứa nhỏ. Việc tính diện tích xung quanh sẽ giúp hiểu rõ về khối lượng chất lỏng có thể được chứa trong phễu và thiết kế sản phẩm chính xác hơn.

Diện tích xung quanh hình nón là một yếu tố quan trọng trong nhiều ứng dụng thực tế liên quan đến thiết kế, sản xuất, tính toán vật liệu và công nghệ. Nó giúp tối ưu hóa việc sử dụng vật liệu, tính toán chi phí và đảm bảo tính hiệu quả của các sản phẩm trong đời sống hàng ngày và các ngành công nghiệp.

Bài viết trên đã giới thiệu về diện tích xung quanh của hình nón, bao gồm công thức tính, ý nghĩa và các ứng dụng thực tế trong đời sống. Hy vọng qua bài viết này, bạn đã có thêm kiến thức hữu ích để áp dụng vào học tập cũng như giải quyết các bài toán liên quan đến hình học không gian.

Đừng quên theo dõi NỘI THẤT HOÀNG GIA để cập nhật những mẫu thiết kế nội thất hiện đại mỗi ngày nhé!

CÔNG TY TNHH SẢN XUẤT NỘI THẤT HOÀNG GIA

Địa chỉ: 106 Tây Sơn, Phường Quang Trung, Quận Đống Đa, Hà Nội

Hotline: 0965 13 68 68

Website: hoanggianoithat.vn