Cấp số nhân là gì? Tổng hợp công thức cấp số nhân

Công thức cấp số nhân

Cấp số nhân là gì?

Cấp số nhân (hay còn gọi là dãy số nhân) là một dãy số trong đó mỗi số hạng sau (số hạng thứ nnn) được tính bằng cách nhân số hạng trước đó (số hạng thứ n−1) với một hằng số không đổi, gọi là công bội (hoặc tỷ lệ).

Định nghĩa

Dãy cấp số nhân được định nghĩa như sau:

• Số hạng đầu tiên được ký hiệu là a₁
• Công bội được ký hiệu là q (với q≠0).
• Các số hạng tiếp theo trong dãy được tính theo công thức:
  aₙ = a₁ ⋅ q⁽ⁿ⁻¹⁾

Trong đó:

• aₙ​ là số hạng thứ n.
• a₁​ là số hạng đầu tiên.
• q là công bội.
• n là chỉ số của số hạng.

Tổng hợp công thức cấp số nhân

Dưới đây là tổng hợp các công thức quan trọng liên quan đến dãy cấp số nhân:

Định nghĩa cấp số nhân

• Một dãy số được gọi là cấp số nhân nếu mỗi số hạng sau (số hạng thứ nnn) được tính bằng cách nhân số hạng trước đó (số hạng thứ n−1) với một hằng số không đổi, gọi là công bội q.

Công thức tổng quát

• Công thức cho số hạng thứ n: aₙ = a₁ ⋅ q⁽ⁿ⁻¹⁾

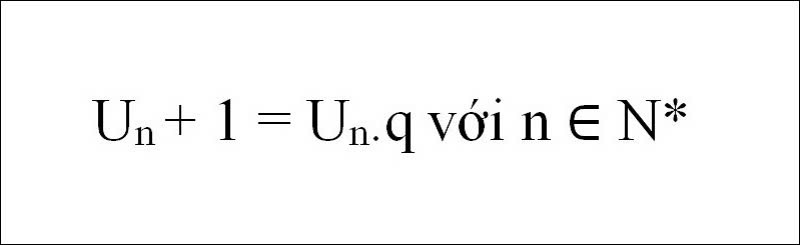
Trong đó:

• aₙ​: Số hạng thứ nnn.
• a₁​: Số hạng đầu tiên.
• q: Công bội.
• n: Chỉ số của số hạng.

Công thức tính tổng của n số hạng

• Tổng của n số hạng đầu tiên trong dãy cấp số nhân được tính bằng công thức: sₙ = a₁ ⋅ (1 – qⁿ) / (1 – q) (nếu q ≠ 1)
• nếu q = 1: sₙ = n ⋅ a₁

Tổng vô hạn (nếu ∣q∣<1)

• Nếu công bội q có giá trị tuyệt đối nhỏ hơn 1, tổng vô hạn của dãy cấp số nhân được tính bằng: s = a₁ / (1 – q)

Một số tính chất của cấp số nhân

• Công bội: Nếu q>1, dãy số tăng; nếu 0<q<1, dãy số giảm; nếu q<0, dãy số sẽ dao động giữa các số dương và âm.
• Cách xác định công bội: Công bội được tính bằng cách chia hai số hạng liên tiếp: q = aₙ / aₙ₋₁

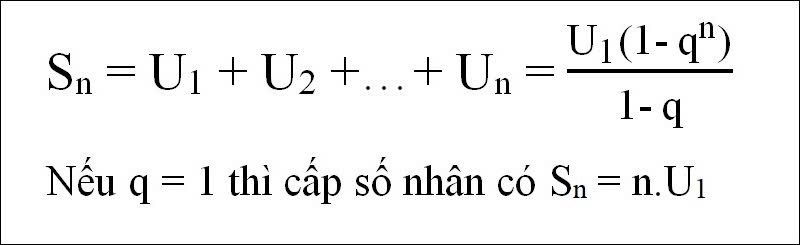
>> Xem thêm: Chu vi hình tam giác

Làm thế nào để giải quyết các bài toán liên quan đến cấp số nhân?

Giải quyết các bài toán liên quan đến cấp số nhân có thể được thực hiện qua một số bước và phương pháp cụ thể. Dưới đây là hướng dẫn chi tiết để giúp bạn giải quyết các bài toán này một cách hiệu quả:

Xác định các thông số cơ bản

Trước tiên, bạn cần xác định các thông số quan trọng của cấp số nhân, bao gồm:

• Số hạng đầu tiên (a₁​): Đây là số hạng đầu tiên của dãy số.
• Công bội (r): Đây là tỷ lệ giữa hai số hạng liên tiếp trong dãy số. Bạn có thể tính công bội bằng cách chia số hạng thứ hai cho số hạng thứ nhất: r = a₂ / a₁

Sử dụng công thức của cấp số nhân

Dựa vào số hạng đầu tiên và công bội, bạn có thể sử dụng các công thức sau để tính toán các giá trị khác trong dãy số:

• Công thức tính số hạng thứ n:
  aₙ = a₁ ⋅ r⁽ⁿ⁻¹⁾
• Công thức tính tổng của n số hạng đầu tiên (nếu r≠1):
  Sₙ = (a₁ * (1 – rⁿ)) / (1 – r) 

Giải bài toán cụ thể

Khi giải bài toán, hãy làm theo các bước sau:

• Đọc kỹ đề bài: Xác định yêu cầu của bài toán, xem cần tìm số hạng nào, tổng bao nhiêu số hạng hoặc các thông tin khác liên quan.
• Lập phương trình: Sử dụng các công thức đã nêu ở trên để lập phương trình phù hợp với thông tin đã cho.
• Tính toán: Thực hiện các phép tính cần thiết để tìm ra kết quả.
• Kiểm tra lại kết quả

Cuối cùng, sau khi tính toán, bạn nên kiểm tra lại kết quả để đảm bảo rằng nó hợp lý và phù hợp với thông tin đã cho trong đề bài. Việc kiểm tra lại giúp giảm thiểu sai sót và củng cố kiến thức của bạn về cấp số nhân.

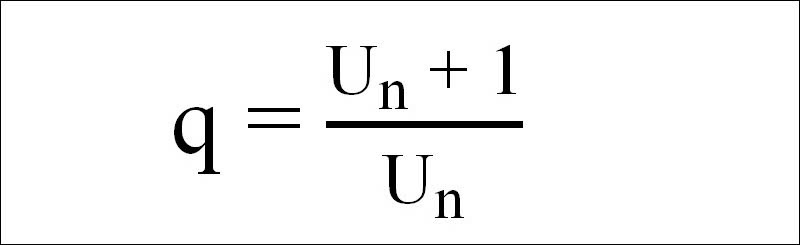
Các dạng bài tập về Công thức cấp số nhân

Dưới đây là một số dạng bài tập phổ biến liên quan đến công thức cấp số nhân, cùng với cách giải và ví dụ minh họa cho từng dạng:

Tìm số hạng trong dãy cấp số nhân

Bài tập: Cho dãy cấp số nhân có số hạng đầu tiên a₁=5 và công bội q=3. Tìm số hạng thứ 4 (a₄​).

Giải:

• Sử dụng công thức: aₙ = a₁ ⋅ q⁽ⁿ⁻¹⁾
• Tính: a₄ = 5 ⋅ 3⁽⁴⁻¹⁾ = 5 ⋅ 3³ = 5 ⋅ 27 = 135

Tính tổng các số hạng trong dãy cấp số nhân

Bài tập: Tính tổng 5 số hạng đầu tiên của dãy cấp số nhân với a₁=2 và q=4

Giải:

• Sử dụng công thức tổng: sₙ = a₁ ⋅ (1 – q) / (1 – qⁿ)
• Tính: s₅ = 2 ⋅ (1 – 4) / (1 – 4⁵) = 2 ⋅ (-3) / (1 – 1024) = 2 ⋅ (-3) / (-1023) = 2 ⋅ 341 = 682

Tìm công bội

Bài tập: Trong dãy số 10,30,90,270,…hãy tìm công bội q.

Giải:

• Tính công bội: q = a₁ / a₂ = 10 / 30 = 3
• Kiểm tra: q = a₃ /a₂ = 90/30  = 3 và  q = a₄/a₃ = 270/90 = 3
• Công bội q=3.

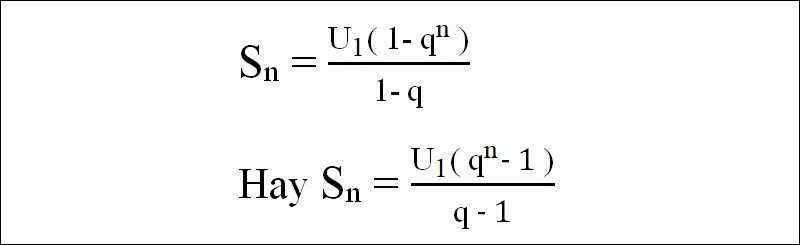
Tính tổng vô hạn

Bài tập: Tính tổng vô hạn của dãy cấp số nhân với a₁=5 và q=½

Giải:

• Sử dụng công thức tổng vô hạn: s = a₁ / (1 – q)
• Tính: s =5/ (1 – 1/2)  = 5/(½) = 5 ⋅ 2 = 10

Tìm số hạng theo điều kiện cho trước

Bài tập: Cho dãy cấp số nhân có a₁=3 và tổng 4 số hạng đầu tiên là 81. Tìm công bội q.

 

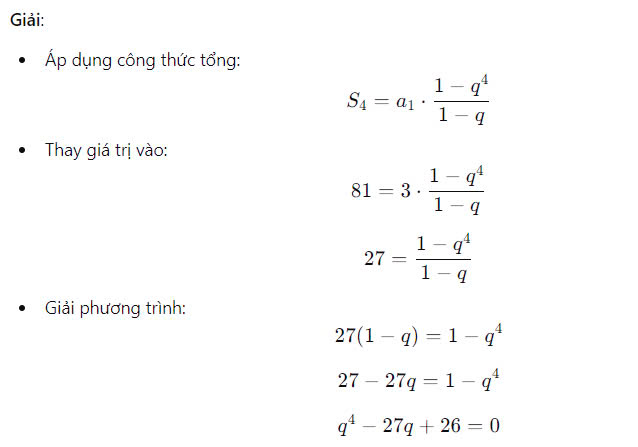
• Sử dụng phương pháp giải phương trình bậc 4 (hoặc thử nghiệm các giá trị) để tìm giá trị của q.

Bài tập tổng hợp

Bài tập: Một nhà đầu tư đầu tư 100 triệu vào một dự án với công suất sinh lợi hàng năm là 10%. Hỏi sau 5 năm, giá trị đầu tư này là bao nhiêu?

Giải:

• Tính giá trị đầu tư sau 5 năm: a₅ = a₁ ⋅ (1 + r)ⁿ = 100 ⋅ (1 + 0.1)⁵
• Tính: a₅ = 100 ⋅ (1.1)⁵ ≈ 100 ⋅ 1.61051 ≈ 161.05 triệu

Bài tập với các số âm

Bài tập: Cho dãy cấp số nhân: −2,6,−18,54,… Tìm số hạng thứ 6 và công bội.

Giải:

• Tính công bội: q =  a₂/ a₁  = 6/ -2 = -3
• Tính số hạng thứ 6: a₆ = a₁ ⋅ q⁵ = -2 ⋅ (-3)⁵ = -2 ⋅ -243 = 486

Tổng kết

Các dạng bài tập trên giúp bạn nắm vững kiến thức về cấp số nhân và cách áp dụng các công thức để giải quyết các bài toán khác nhau. Hy vọng bài viết trên về Công thức cấp số nhân sẽ giúp ích được cho bạn!

Đừng quên theo dõi NỘI THẤT HOÀNG GIA để cập nhật những mẫu thiết kế nội thất hiện đại mỗi ngày nhé!

>> Tham khảo: Báo giá tủ bếp gỗ