Công Thức Tính Chu Vi Hình Tam Giác Đơn Giản Dễ Nhớ

Hình tam giác là gì?

Hình tam giác là một đa giác có ba cạnh và ba đỉnh. Tam giác là hình cơ bản nhất trong hình học phẳng, và tất cả các tam giác đều có tổng các góc bằng 180 độ. Một tam giác có thể được phân loại theo độ dài cạnh và số đo góc.

 

Các loại tam giác:

Theo độ dài cạnh:

Tam giác đều: Cả ba cạnh bằng nhau, mỗi góc đều bằng 60 ∘ .

Tam giác cân: Có hai cạnh bằng nhau, hai góc ở đáy bằng nhau.

Tam giác thường: Không có cạnh nào bằng nhau.

Theo góc:

Tam giác vuông: Có một góc vuông (90 ∘).

Tam giác tù: Có một góc lớn hơn Tam giác nhọn: Cả ba góc đều nhỏ hơn 90 ∘

Học sinh lớp 2 trong giờ học toán

Công thức tính chu vi hình tam giác

Với mỗi loại tam giác cụ thể thì chúng ta sẽ có những công thức tính toán chu vi khác nhau, theo đó công thức tính chu vi của mỗi loại tam giác được thể hiện như sau:

Công thức tính chu vi tam giác thường

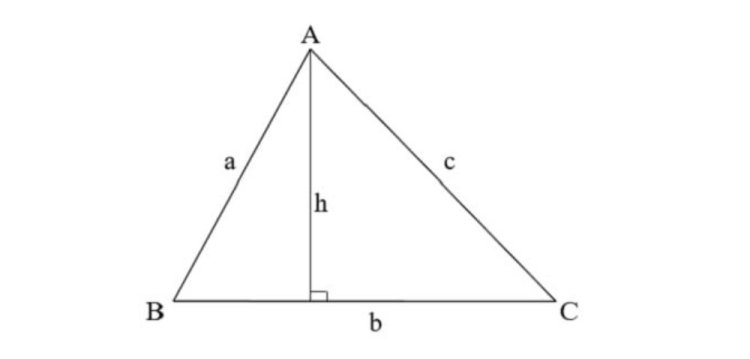
Tam giác thường là tam giác cơ bản và học sinh thường gặp nhất, nó có đặc điểm là các góc, các cạnh bên không bằng nhau. Theo đó, chu vi hình tam giác sẽ được tính bằng tổng độ dài ba cạnh của tam giác đó. Ta có công thức: P = a + b + c

 

Trong đó:

 

P: chu vi hình tam giác

a, b, c: độ dài ba cạnh của tam giác

 

Công thức tính chu vi tam giác cân

Tam giác cân là tam giác có hai cạnh, hai góc bằng nhau , ta có công thức tính chu vi tam giác cân: P = 2.a + c

Trong đó:

P: chu vi hình tam giác

a: độ dài hai cạnh bên của tam giác cân

c: độ dài cạnh đáy của tam giác cân

 

Công thức tính chu vi tam giác đều

Tam giác đều là tam giác có ba cạnh, ba góc nhọn bằng nhau, đây cũng chính là trường hợp đặc biệt của tam giác cân, ta có công thức tính chu vi tam giác đều: P = a + a + a = 3 x a

Trong đó:

P: chu vi của tam giác đều

a: độ dài cạnh của tam giác đều

Hình tam giác

Công thức tính chu vi tam giác vuông

Tam giác vuông là tam giác có một góc vông bằng 90 độ, ta có công thức tính chu vi tam giác vuông: P = a + b + c

Trong đó:

P: chu vi của tam giác vuông

a, b: độ dài của hai cạnh tam giác vuông

c: độ dài cạnh huyền của tam giác vuông

 Công thức tính chu vi hình tam giác vuông cân

Tam giác vuông cân là loại tam giác đặc biệt mang tính chất của cả hai loại tam giác đó là tam giác vông và tam giác cân, theo đó tam giác vuông cân sẽ có hai cạnh góc vuông có độ dài bằng nhau và hai góc nhọn có số đo là 45 độ. Ta có công thức tính chu vi tam giác vuông cân: P = 2a + c

Trong đó:

P: chu vi của tam giác vuông cân

a: độ dài của hai cạnh bên hình tam giác vuông cân

c: độ dài cạnh đáy của hình tam giác vuông cân

>> Xem thêm: Công thức cấp số nhân

Giờ học toán trên lớp

Ứng dụng công thức tính chu vi tam giác

Công thức tính chu vi tam giác không chỉ có ý nghĩa trong toán học mà còn được áp dụng rộng rãi trong nhiều lĩnh vực thực tế. Dưới đây là một số ứng dụng phổ biến:

Xây dựng và kiến trúc:

Thiết kế công trình: Khi xây dựng các công trình có dạng tam giác, như mái nhà hoặc cầu, cần phải tính chu vi để ước lượng số vật liệu cần sử dụng (như dây cáp, gỗ, thép).

Thi công đường: Với các công trình đường giao thông có dạng tam giác, chu vi sẽ giúp tính toán độ dài các cạnh, từ đó xác định được diện tích cần rải nhựa hoặc bê tông.

Thiết kế và cắt may:

May quần áo, cắt vải: Trong thiết kế thời trang, nếu một mẫu trang phục có phần hình tam giác (ví dụ như khăn choàng, nắp váy), việc tính chu vi giúp đo lường số lượng vải cần thiết hoặc xác định kích thước các mảnh cắt.

Công nghiệp và kỹ thuật:

Chế tạo máy móc: Trong kỹ thuật cơ khí, nhiều bộ phận máy móc có dạng tam giác hoặc có các mặt tam giác, cần tính chu vi để xác định chiều dài các bộ phận ghép nối, dây dẫn hay các thành phần khác.

Thiết kế và lắp ráp khung giàn: Đối với các công trình xây dựng hoặc kết cấu dạng giàn tam giác, việc tính chu vi giúp ước tính chiều dài thanh giằng, cột thép cần thiết cho kết cấu.

Đo đạc và địa chất:

Định vị trong địa lý: Trong việc đo đạc địa lý hoặc định vị vị trí trên bản đồ, các khu vực hình tam giác có thể cần tính chu vi để tính toán đường biên, diện tích khu vực hoặc quãng đường di chuyển.

Khảo sát và đo đạc đất đai: Trong quá trình đo đạc đất đai, nhiều thửa đất có hình tam giác. Tính chu vi sẽ giúp xác định ranh giới, từ đó tính diện tích, phục vụ cho các mục đích khai thác, xây dựng.

Thiết kế đồ họa và kỹ thuật số:

Xây dựng mô hình 3D: Trong thiết kế đồ họa 3D hoặc mô phỏng kỹ thuật, các hình tam giác thường là đơn vị cơ bản để xây dựng mô hình phức tạp hơn. Tính chu vi giúp các nhà thiết kế kiểm soát kích thước và độ chính xác của mô hình.

Toán học và giáo dục:

Bài toán thực hành: Học sinh thường được yêu cầu tính chu vi tam giác trong các bài toán thực hành, giúp nắm vững kiến thức về hình học và ứng dụng nó vào thực tế.

Ứng dụng trong vật lý:

Phân tích lực: Trong các bài toán phân tích lực (ví dụ như cấu trúc chịu lực tam giác trong vật lý), tính chu vi giúp xác định khoảng cách, từ đó giúp tính toán lực tác dụng trên các điểm khác nhau của kết cấu.

Thiết kế cảnh quan và trang trí:

Thiết kế khu vườn hoặc công viên: Nếu một khu vườn hoặc một phần của công viên có hình dạng tam giác, tính chu vi sẽ giúp ước tính chiều dài hàng rào hoặc các đường bao quanh khu vực này.

Thiết kế nội thất:

Tạo các chi tiết trang trí: Trong trang trí nội thất, các chi tiết hình tam giác (như tấm kính, gương, đèn) có thể cần được tính chu vi để đo chính xác vật liệu cần dùng cho khung viền hoặc thiết kế.

Những ứng dụng này cho thấy công thức tính chu vi tam giác được sử dụng trong rất nhiều tình huống thực tế, giúp con người đo lường, tính toán và giải quyết nhiều vấn đề trong cuộc sống hàng ngày.

>> Tham khảo: Mẫu tủ bếp gỗ đẹp hiện đại