Diện tích toàn phần hình trụ: Công thức vàng và bài tập thực tế

Diện tích toàn phần hình trụ

Khái niệm cơ bản về hình trụ

Để hiểu rõ về diện tích hình trụ, trước tiên chúng ta cần nắm vững những kiến thức cơ bản về hình trụ.

Hình trụ là gì?

Trong không gian ba chiều, hình trụ được định nghĩa là hình được tạo thành khi ta quay một hình chữ nhật quanh một trong các cạnh của nó. Cạnh mà hình chữ nhật quay quanh được gọi là trục của hình trụ.

Các yếu tố cấu thành hình trụ: đáy, mặt xung quanh, đường sinh

Một hình trụ hoàn chỉnh bao gồm các thành phần sau:

Hai đáy: Là hai hình tròn hoàn toàn giống nhau và song song với nhau. Bán kính của hình tròn đáy được ký hiệu là r.

Mặt xung quanh: Là phần bề mặt bao quanh hai đáy. Nếu bạn trải mặt xung quanh của hình trụ ra, bạn sẽ được một hình chữ nhật. Chiều dài của hình chữ nhật này bằng chu vi của đường tròn đáy (2πr) và chiều rộng của nó bằng chiều cao của hình trụ (ký hiệu là h).

Đường sinh: Là các đoạn thẳng nối hai điểm tương ứng trên hai đường tròn đáy và song song với trục của hình trụ. Chiều dài của đường sinh chính bằng chiều cao h của hình trụ.

Phân loại hình trụ thường gặp

Trong chương trình học và ứng dụng thực tế, chúng ta thường gặp hai loại hình trụ chính:

Hình trụ tròn: Đây là loại hình trụ mà hai đáy là hình tròn. Khi nói đến “hình trụ” một cách thông thường, người ta thường ngầm hiểu là hình trụ tròn.

Hình trụ xiên: Là hình trụ có trục không vuông góc với mặt đáy. Trong phạm vi bài viết này, chúng ta sẽ tập trung chủ yếu vào hình trụ tròn, vì đây là dạng phổ biến nhất.

Hình trụ

Công thức tính diện tích toàn phần hình trụ – Giải thích chi tiết

Diện tích đáy hình trụ được tính như thế nào?

Như đã đề cập, đáy của hình trụ là một hình tròn. Công thức tính diện tích của một hình tròn là:

Diện tích đáy = π * r²

Vì hình trụ có hai đáy hoàn toàn giống nhau, nên tổng diện tích của hai đáy sẽ là:

Diện tích hai đáy = 2 * π * r²

Diện tích xung quanh hình trụ được tính ra sao?

Để tính diện tích xung quanh của hình trụ, bạn có thể hình dung việc trải mặt xung quanh của hình trụ ra thành một hình chữ nhật. Chiều dài của hình chữ nhật này chính là chu vi của đường tròn đáy, tức là 2πr. Chiều rộng của hình chữ nhật này chính là chiều cao của hình trụ, tức là h.

Vậy, diện tích xung quanh của hình trụ được tính bằng công thức:

Diện tích xung quanh = Chu vi đáy * Chiều cao = 2π * r * h

Công thức tổng quát cho diện tích hình trụ

Từ những phân tích trên, chúng ta có thể dễ dàng suy ra công thức tính diện tích toàn phần hình trụ:

Diện tích toàn phần = Diện tích hai đáy + Diện tích xung quanh

Diện tích toàn phần = 2πr² + 2πrh

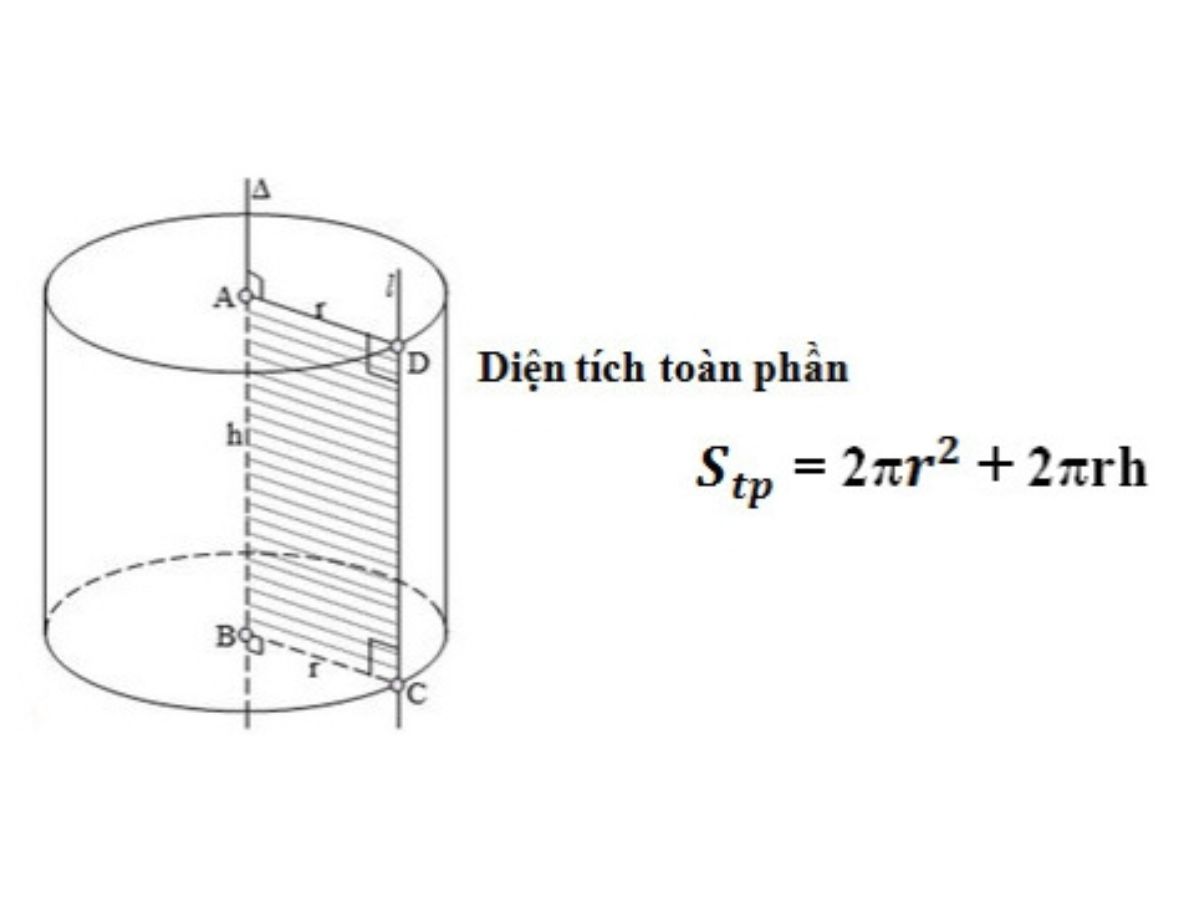
Công thức hình trụ

Hướng dẫn từng bước tính diện tích hình trụ kèm ví dụ minh họa

Các bước cơ bản để tính diện tích toàn phần

Để tính diện tích hình trụ, bạn cần thực hiện theo các bước sau:

Xác định bán kính đáy (r) và chiều cao (h) của hình trụ. Thông thường, các giá trị này sẽ được cho trong đề bài.

Tính diện tích của hai đáy: Sử dụng công thức 2πr².

Tính diện tích xung quanh: Sử dụng công thức 2πrh.

Tính tổng diện tích toàn phần: Cộng diện tích hai đáy và diện tích xung quanh lại với nhau.

Ví dụ 1: Tính diện tích toàn phần khi biết bán kính và chiều cao

Đề bài: Một hình trụ có bán kính đáy là 5 cm và chiều cao là 10 cm. Tính diện tích hình trụ này.

Giải:

Xác định các giá trị:

Bán kính đáy (r) = 5 cm

Chiều cao (h) = 10 cm

Tính diện tích hai đáy:

Diện tích một đáy = π * (5 cm)² = 25π cm²

Diện tích hai đáy = 2 * 25π cm² = 50π cm²

Tính diện tích xung quanh:

Diện tích xung quanh = 2 * π * (5 cm) * (10 cm) = 100π cm²

Tính diện tích toàn phần:

Diện tích toàn phần = Diện tích hai đáy + Diện tích xung quanh = 50π cm² + 100π cm² = 150π cm²

Vậy, diện tích toàn phần hình trụ trong trường hợp này là 150π cm², hoặc xấp xỉ 471.24 cm² (nếu lấy π ≈ 3.1416).

Ví dụ 2: Bài toán thực tế về diện tích hình trụ

Đề bài: Một công ty muốn sản xuất các lon sữa hình trụ có chiều cao 12 cm và đường kính đáy là 8 cm. Tính lượng vật liệu cần thiết để làm một chiếc lon sữa (bỏ qua phần mép nối).

Giải:

Xác định các giá trị:

Chiều cao (h) = 12 cm

Đường kính đáy = 8 cm => Bán kính đáy (r) = 8 cm / 2 = 4 cm

Tính diện tích hai đáy:

Diện tích một đáy = π * (4 cm)² = 16π cm²

Diện tích hai đáy = 2 * 16π cm² = 32π cm²

Tính diện tích xung quanh:

Diện tích xung quanh = 2 * π * (4 cm) * (12 cm) = 96π cm²

Tính diện tích toàn phần:

Diện tích toàn phần = Diện tích hai đáy + Diện tích xung quanh = 32π cm² + 96π cm² = 128π cm²

Vậy, lượng vật liệu cần thiết để làm một chiếc lon sữa là 128π cm², hoặc xấp xỉ 402.12 cm².

Hình trụ

Ứng dụng thực tế của diện tích toàn phần hình trụ trong đời sống và kỹ thuật

Trong lĩnh vực xây dựng và kiến trúc

Trong xây dựng, việc tính toán diện tích toàn phần hình trụ cần thiết khi xác định lượng vật liệu cần thiết để xây dựng các cột trụ tròn, ống dẫn nước, hoặc các cấu trúc hình trụ khác. Điều này giúp các kỹ sư và kiến trúc sư dự toán chi phí và đảm bảo tính thẩm mỹ cũng như độ bền của công trình.

Trong ngành sản xuất và thiết kế

Trong ngành sản xuất, đặc biệt là sản xuất bao bì, việc tính toán diện tích hình trụ giúp các nhà sản xuất xác định lượng vật liệu cần thiết để tạo ra các sản phẩm như lon đồ uống, hộp đựng thực phẩm, hoặc các loại ống dẫn. Việc tính toán chính xác giúp tối ưu hóa chi phí sản xuất và giảm thiểu lãng phí vật liệu.

Qua bài viết này, chúng tôi hy vọng bạn đã nắm vững khái niệm, công thức và cách tính diện tích toàn phần hình trụ. Việc hiểu rõ công thức diện tích hình trụ và luyện tập giải các bài tập liên quan sẽ giúp bạn tự tin hơn trong môn Toán học và có thể ứng dụng kiến thức này vào giải quyết các vấn đề thực tế. Nếu bạn có bất kỳ câu hỏi nào khác, đừng ngần ngại liên hệ với chúng tôi. Chúc bạn học tập thật tốt!