Cách nhận diện hình trụ, công thức diện tích toàn phần hình trụ​

Diện tích toàn phần hình trụ

Hình trụ: Khái niệm và phân loại

Hình trụ là gì?

Hình trụ là một hình khối không gian được tạo thành khi ta quay một hình chữ nhật quanh một cạnh cố định của nó. Hình trụ có hai đáy là hai hình tròn bằng nhau và song song với nhau, được nối với nhau bởi một mặt cong gọi là mặt trụ.

Các thành phần chính của hình trụ

Hai đáy: Là hai hình tròn bằng nhau và song song.

Mặt trụ: Là phần mặt cong nối liền hai đáy.

Trục: Là đường thẳng vuông góc với hai đáy và đi qua tâm của chúng.

Đường sinh: Là đoạn thẳng nối hai điểm tương ứng trên hai đường tròn đáy.

Cách nhận diện hình trụ

Để nhận biết một hình trụ, bạn có thể dựa vào các đặc điểm sau:

Hai đáy hình tròn: Hình trụ luôn có hai đáy là hình tròn bằng nhau và song song.

Mặt cong trơn tru: Mặt nối liền hai đáy là một mặt cong trơn tru.

Trục vuông góc với đáy: Trục của hình trụ luôn vuông góc với hai đáy.

Có mấy loại hình trụ?

Về cơ bản, tất cả các hình trụ đều có cùng cấu tạo như đã mô tả ở trên. Tuy nhiên, dựa vào một số yếu tố khác nhau, người ta có thể phân loại hình trụ thành các loại khác nhau như:

Hình trụ tròn đều: Là loại hình trụ phổ biến nhất, trong đó hai đáy là hình tròn và trục vuông góc với mặt phẳng chứa hai đáy.

Hình trụ ellip: Hai đáy của hình trụ này là các hình elip đồng dạng và cùng trục.

Hình trụ nghiêng: Trục của hình trụ không vuông góc với mặt phẳng chứa hai đáy.

>> Xem thêm: Diện tích xung quanh hình nón​

Hình trụ

Công thức về thể tích, diện tích xung quanh, diện tích toàn phần hình trụ

Diện tích đáy (Sđáy)

Ý nghĩa: Đây là diện tích của một trong hai đáy hình tròn.

Công thức: Sđáy = πR²

Diện tích xung quanh (Sxq)

Ý nghĩa: Đây là diện tích của phần mặt cong bao quanh hình trụ.

Công thức: Sxq = 2πRh

Trong đó:

h: Chiều cao của hình trụ

Nếu bạn cắt dọc hình trụ và trải phẳng phần mặt cong ra, bạn sẽ được một hình chữ nhật. Chiều dài của hình chữ nhật này bằng chu vi đường tròn đáy (2πR) và chiều rộng bằng chiều cao của hình trụ (h).

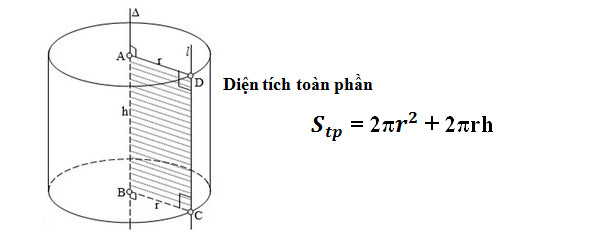
Diện tích toàn phần hình trụ (Stp)

Ý nghĩa: Đây là tổng diện tích của tất cả các mặt của hình trụ, bao gồm cả hai đáy và phần mặt cong.

Công thức: Stp = Sxq + 2Sđáy = 2πRh + 2πR²

Thể tích (V)

Ý nghĩa: Đây là lượng không gian mà hình trụ chiếm.

Công thức: V = Sđáy . h = πR²h

Công thức hình trụ

Bài tập về các công thức tính thể tích, diện tích toàn phần hình trụ

Bài toán 1

Một hình trụ có bán kính đáy là 5cm và chiều cao là 12cm. Tính:

Diện tích xung quanh

Diện tích toàn phần

Thể tích

Bài toán 2

Một ống nước hình trụ có đường kính trong là 20cm và chiều dài là 5m. Tính thể tích nước mà ống nước có thể chứa.

Bài toán 3

Một hình trụ có diện tích xung quanh bằng 314 cm² và chiều cao bằng bán kính đáy. Tính bán kính của đáy từ đó suy ra thể tích của hình trụ.

Bài toán 4

Một hình trụ có diện tích toàn phần gấp 3 lần diện tích xung quanh. Tính tỉ số giữa chiều cao và bán kính đáy của hình trụ.

Bài toán 5

Một hình trụ nội tiếp trong một hình cầu có bán kính R. Tìm chiều cao của hình trụ để thể tích của nó lớn nhất.

Bài toán 6

Cho một hình trụ có bán kính đáy là R. Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng R/2. Tính diện tích thiết diện.

Bài toán 7

Một hình trụ có bán kính đáy bằng R. Một mặt phẳng cắt hình trụ theo một thiết diện là hình chữ nhật ABCD có AB là đường kính của đường tròn đáy. Biết AB = 2AD. Tính thể tích lớn nhất của khối trụ.

Bài toán 8

Cho hình trụ có bán kính đáy bằng R. Một hình nón có đỉnh là tâm của một đáy và đáy của hình nón trùng với đáy còn lại của hình trụ. Tỉ số thể tích giữa hình nón và hình trụ là bao nhiêu?

Giải nhiều bài tập để thành thạo hình trụ hơn nhé!

Hướng dẫn giải

Trong quá trình giải, sẽ sử dụng giá trị xấp xỉ của pi là 3.14 để tính toán nhé!

Bài toán 1

Diện tích xung quanh: Sxq = 2πRh = 2 * 3.14 * 5 * 12 = 376.8 cm²

Diện tích toàn phần: Stp = 2πRh + 2πR² = 376.8 + 2 * 3.14 * 5² = 533.8 cm²

Thể tích: V = πR²h = 3.14 * 5² * 12 = 942 cm³

Bài toán 2

Bán kính trong: R = 20/2 = 10 cm

Chiều cao: h = 500 cm (đổi 5m = 500cm)

Thể tích: V = πR²h = 3.14 * 10² * 500 = 1570000 cm³ = 1.57 m³

Bài toán 3

Ta có: Sxq = 2πRh = 314 cm² và h = R

=> 2πR² = 314 => R² ≈ 50 => R ≈ 7.07 cm

Thể tích: V = πR²h = π * 7.07² * 7.07 ≈ 1110.25 cm³

Bài toán 4

Stp = 3Sxq => 2πRh + 2πR² = 3 * 2πRh

=> R = h

Tỉ số h/R = 1

Bài toán 5

Để thể tích hình trụ nội tiếp hình cầu lớn nhất thì hình trụ phải có chiều cao bằng đường kính của hình cầu.

Vậy chiều cao h = 2R

Bài toán 6

Thiết diện là hình chữ nhật có chiều dài bằng chu vi đường tròn đáy và chiều rộng bằng khoảng cách từ mặt phẳng cắt đến trục hình trụ.

Diện tích thiết diện = 2πR * (R/2) = πR²

Bài toán 7

Gọi O là tâm đường tròn đáy. Ta có tam giác AOD vuông tại O.

Áp dụng định lý Pytago: AD² = AO² + OD² = R² + (R/2)² = 5R²/4

Thể tích hình trụ: V = πR²h = πR² * 2AD = πR² * 2√(5R²/4) = √5πR³

Để V lớn nhất thì R lớn nhất, tức là hình chữ nhật ABCD trở thành hình vuông.

Bài toán 8

Thể tích hình nón: Vn = (1/3)πR²h

Thể tích hình trụ: Vt = πR²h

Tỉ số Vn/Vt = (1/3)

Trên đây là một số thông tin về chủ đề hình trụ, gồm các công thức về thể tích, diện tích toàn phần hình trụ. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.

>> Xem thêm: Báo giá thi công nội thất gỗ óc chó