Hình nón là gì? Công thức tính thể tích diện tích xung quanh hình nón​

Diện tích xung quanh hình nón

Hình nón là gì và cách nhận biết?

Hình nón là gì?

Hình nón là một hình khối quen thuộc trong cuộc sống hàng ngày. Bạn có thể dễ dàng hình dung hình nón qua những vật dụng như:

Mũ chóp: Phần trên của chiếc mũ chóp thường có hình dạng của một hình nón.

Kem ốc quế: Phần đựng kem của chiếc ốc quế cũng là một hình nón.

Phễu: Phễu để rót chất lỏng thường có hình dạng nón.

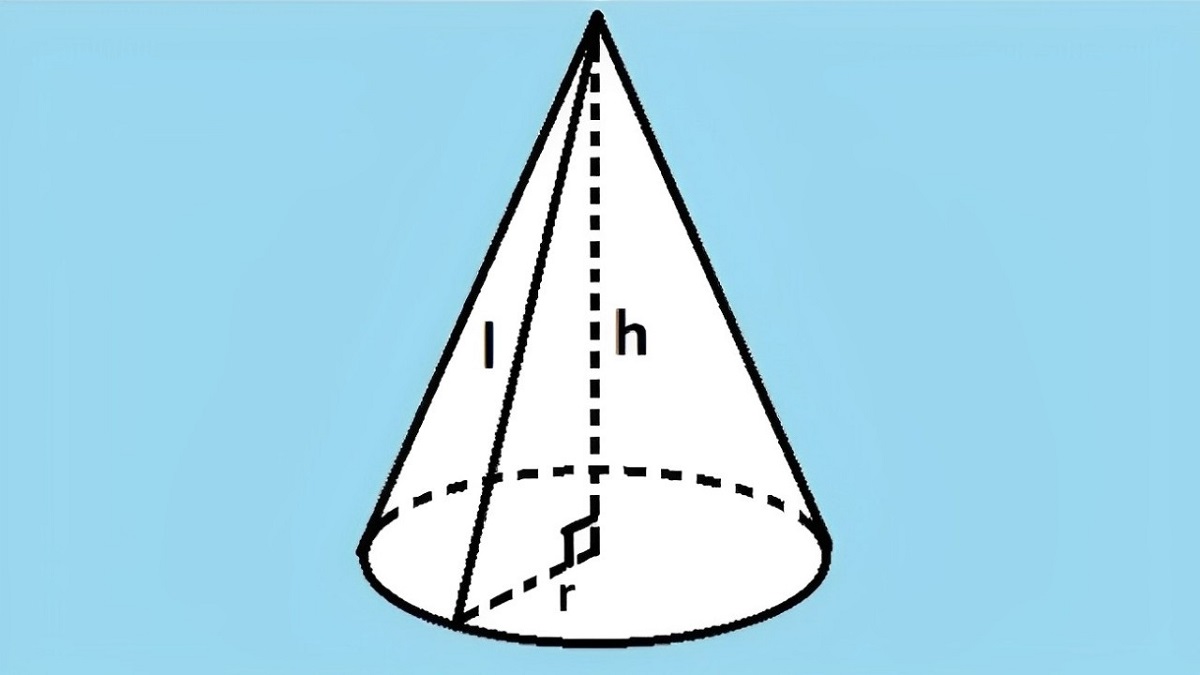
Về mặt hình học: Hình nón là một hình khối ba chiều được tạo thành khi quay một tam giác vuông quanh một cạnh góc vuông cố định.

Các thành phần của hình nón

Đỉnh: Điểm cao nhất của hình nón.

Đáy: Hình tròn ở phía dưới của hình nón.

Đường sinh: Đường thẳng nối đỉnh với bất kỳ điểm nào trên đường tròn đáy.

Chiều cao: Đoạn thẳng vuông góc kẻ từ đỉnh xuống tâm của đáy.

Cách nhận biết hình nón

Để nhận biết một hình nón, bạn hãy quan sát xem hình đó có các đặc điểm sau hay không:

Có một đỉnh nhọn: Đây là đặc điểm dễ nhận biết nhất của hình nón.

Có một đáy hình tròn: Đáy của hình nón luôn là một hình tròn.

Các đường sinh đều bằng nhau: Tất cả các đường sinh của hình nón đều có độ dài bằng nhau.

Hình dáng thuôn nhọn dần từ đáy lên đỉnh: Hình nón có dạng hình chóp tròn đều.

>> Xem thêm: Diện tích toàn phần hình trụ​

Hình nón

Công thức tính diện tích xung quanh hình nón, thể tích hình nón và các công thức liên quan

Các công thức tính toán cho hình nón

Giả sử ta có một hình nón với:

r: Bán kính đáy

h: Chiều cao

l: Đường sinh (đoạn thẳng nối đỉnh với một điểm bất kỳ trên đường tròn đáy)

Diện tích xung quanh hình nón

Công thức: Sxq = πrl

Ý nghĩa: Diện tích xung quanh của hình nón bằng tích của pi (π), bán kính đáy (r) và đường sinh (l).

Diện tích đáy của hình nón

Công thức: Sđáy = πr²

Ý nghĩa: Diện tích đáy của hình nón (là một hình tròn) bằng bình phương bán kính nhân với pi.

Diện tích toàn phần (Stp)

Công thức: Stp = Sxq + Sđáy = πrl + πr²

Ý nghĩa: Diện tích toàn phần bằng tổng diện tích xung quanh và diện tích đáy.

Thể tích (V)

Công thức: V = 1/3πr²h

Ý nghĩa: Thể tích hình nón bằng một phần ba tích của pi, bình phương bán kính đáy và chiều cao.

Lưu ý

Đường sinh (l): Có thể tính được đường sinh dựa vào bán kính đáy và chiều cao bằng định lý Pytago: l² = r² + h²

Pi (π): Là một hằng số toán học xấp xỉ bằng 3.14.

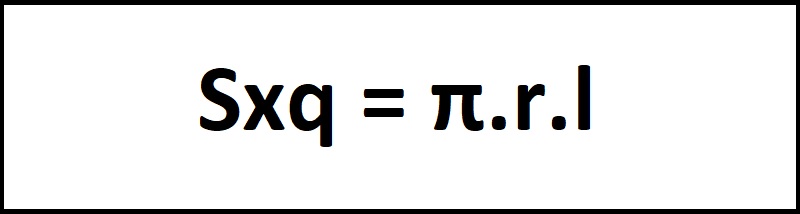
Công thức về hình nón

Một số bài tập về diện tích xung quanh hình nón, thể tích và hướng dẫn giải

Bài tập 1

Một hình nón có bán kính đáy là 6cm và chiều cao là 8cm. Hãy tính:

Diện tích xung quanh

Diện tích toàn phần

Thể tích

Giải:

Bước 1: Tính đường sinh: l² = r² + h² = 6² + 8² = 100 => l = 10cm

Bước 2: Tính diện tích xung quanh: Sxq = πrl = 3.14 x 6 x 10 ≈ 188.4 cm²

Bước 3: Tính diện tích toàn phần: Stp = πrl + πr² = 188.4 + 3.14 x 6² ≈ 251.2 cm²

Bước 4: Tính thể tích: V = 1/3πr²h = 1/3 x 3.14 x 6² x 8 ≈ 301.44 cm³

Đáp số:

Diện tích xung quanh: 188.4 cm²

Diện tích toàn phần: 251.2 cm²

Thể tích: 301.44 cm³

Bài tập 2

Một hình nón có diện tích xung quanh là 157 cm² và đường sinh là 10cm. Tính bán kính đáy và thể tích của hình nón.

Giải:

Bước 1: Tính bán kính đáy: Sxq = πrl => r = Sxq / (πl) = 157 / (3.14 x 10) ≈ 5 cm

Bước 2: Tính chiều cao: l² = r² + h² => h² = l² – r² = 10² – 5² = 75 => h ≈ 8.66 cm

Bước 3: Tính thể tích: V = 1/3πr²h ≈ 1/3 x 3.14 x 5² x 8.66 ≈ 226.19 cm³

Đáp số:

Bán kính đáy: 5 cm

Thể tích: 226.19 cm³

Bài tập 3: Một bài toán thực tế

Một chiếc mũ hình nón có đường kính đáy là 28cm và chiều cao là 25cm. Tính diện tích vải cần dùng để làm mũ, bỏ qua mép gấp.

Hướng dẫn giải: 

Diện tích vải cần dùng chính là diện tích xung quanh của hình nón.

Bài toán 4: Một bài toán kết hợp hình nón và hình cầu

Một hình nón có đường sinh bằng 10cm và góc ở đỉnh bằng 60 độ. Người ta nội tiếp hình nón một hình cầu sao cho hình cầu tiếp xúc với tất cả các mặt của hình nón. Tính:

Bán kính của hình cầu.

Thể tích phần không gian nằm bên trong hình nón nhưng bên ngoài hình cầu.

Hướng dẫn giải: 

Sử dụng kiến thức về tam giác đều và tính chất tiếp xúc của hình cầu với hình nón để tìm mối quan hệ giữa bán kính hình cầu và các yếu tố của hình nón.

Tính thể tích hình nón và hình cầu, sau đó trừ đi để tìm thể tích phần không gian cần tìm.

Luyện tập nhiều để hình học không gian không còn là nỗi sợ

Cách học giúp hình học không gian dễ thở hơn

Nắm vững lý thuyết

Tìm hiểu các khái niệm cơ bản: Điểm, đường thẳng, mặt phẳng, hình chiếu, góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng,…

Hiểu rõ các định lý: Định lý Pytago trong không gian, định lý về đường thẳng vuông góc với mặt phẳng, định lý về hai mặt phẳng vuông góc,…

Vẽ hình minh họa: Khi học một định lý mới, hãy vẽ hình minh họa để trực quan hóa và hiểu rõ hơn.

Rèn luyện tư duy không gian

Xây dựng mô hình: Sử dụng các vật dụng xung quanh như hộp giấy, que tăm để tạo ra các mô hình hình học không gian.

Chơi các trò chơi: Các trò chơi như Rubik, xếp hình 3D sẽ giúp bạn rèn luyện khả năng xoay chuyển hình khối trong không gian.

Quan sát các vật thể xung quanh: Hãy quan sát các vật thể trong cuộc sống hàng ngày để tìm thấy các hình khối không gian.

Làm bài tập

Bắt đầu từ các bài tập cơ bản: Làm quen với cách vẽ hình, xác định các yếu tố hình học, và áp dụng các định lý.

Tăng dần độ khó: Khi đã thành thạo các bài tập cơ bản, hãy chuyển sang các bài tập phức tạp hơn, đòi hỏi tư duy trừu tượng hơn.

Làm các bài tập trắc nghiệm: Để làm quen với dạng bài thi và rèn luyện tốc độ làm bài.

Trên đây là một số thông tin về chủ đề thể tích, diện tích xung quanh hình nón. Hi vọng các bạn đã có cho mình thông tin hữu ích.

>> Xem thêm: Xưởng sản xuất nội thất gỗ óc chó